目次
二分探索木(にぶんたんさくぎ)
木構造とは
木構造(きこうぞう)とは、データ構造の1つで木のような階層構造でデータを管理するものです。
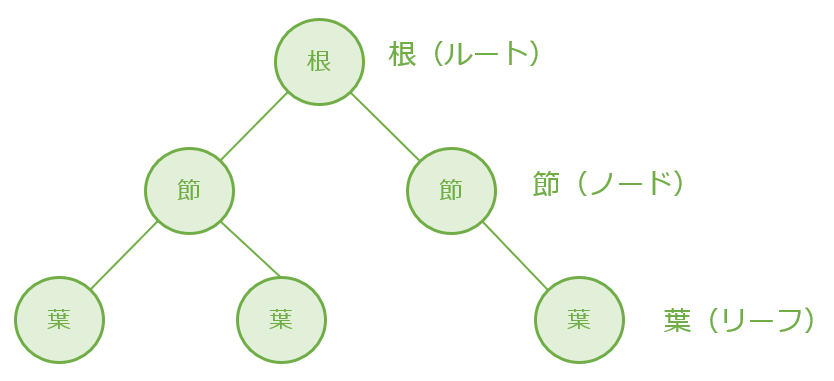
木構造の要素部分を節(ノード)といい、親のない最上位のノードを根(ルート)、子のないノードを葉(リーフ)、そして ノードとノードを繋ぐ線のことを枝(ブランチ)といいます。
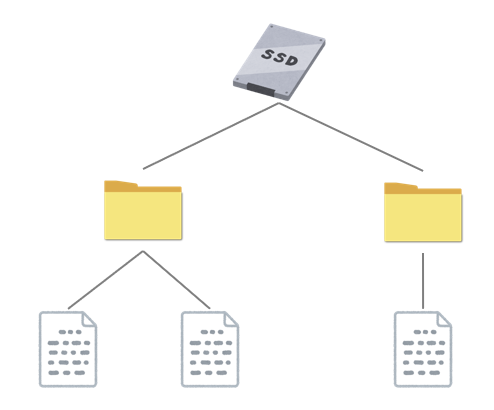
木構造は、ハードディスクのファイルシステムやインターネットのドメイン名などの管理で使用されています。
二分探索木とは
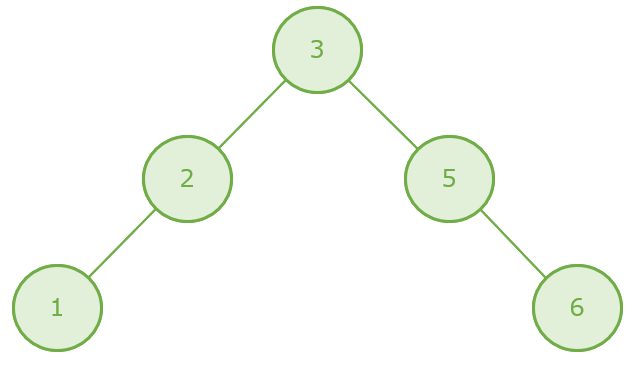
二分探索木(英:binary search tree)とは、木構造の左部分と右部分の関係が「左の子 < 親 < 右の子」になっている二分木のことです。

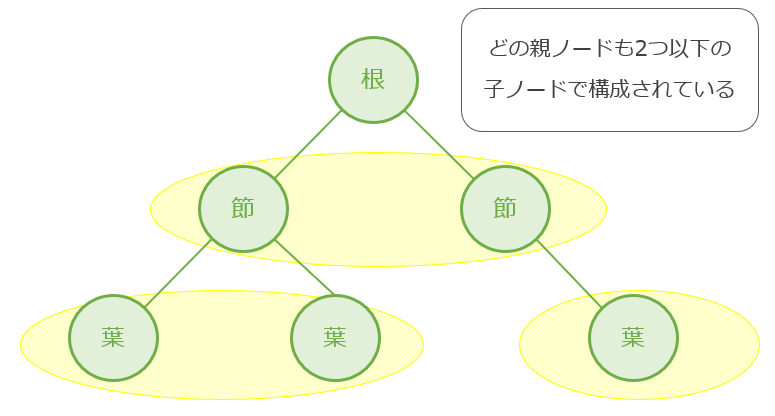
二分探索木は、木構造の左部分と右部分の関係が「左の子 < 親 < 右の子」となっているので、例えば数値「1」~「6」を二分探索木にあてはめると次のように格納されます。
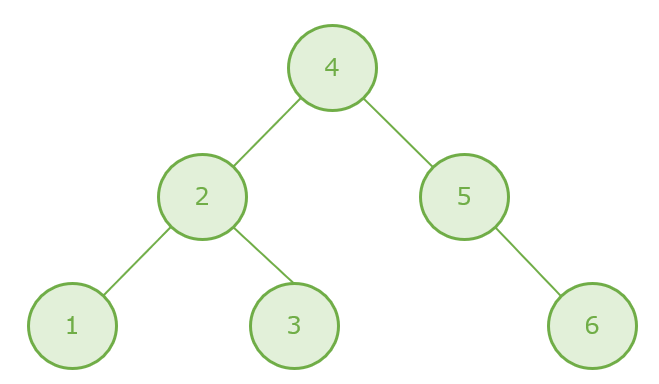
二分探索木の操作
スポンサーリンク
二分探索木からデータを探索する
二分探索木は「左の子 < 親 < 右の子」の順にデータが並んでいるので、ルートから順に比較していき、探索対象の方が小さければ左へ、探索対象の方が大きければ右へ移動することで、探索を容易に行うことができます。
例として次の二分探索木から「3」を探索します。
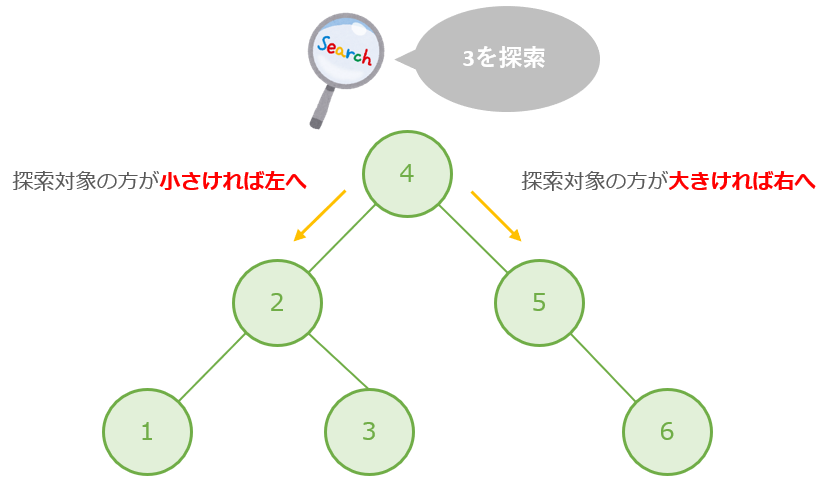
探索の流れ
- 「3」とルート「4」を比較し「3」の方が小さいので左へ
- 「3」とノード「2」を比較し「3」の方が大きいので右へ
- 「3」とノード「3」を比較、一致したので探索終了
二分探索木にデータを追加する
二分探索木にデータを追加する場合は、データを探索する場合と同じでルートから順に比較していき、追加要素の方が小さければ左へ、追加要素の方が大きければ右へ移動する操作を繰り返し比較対象がなくなった場所に追加します。
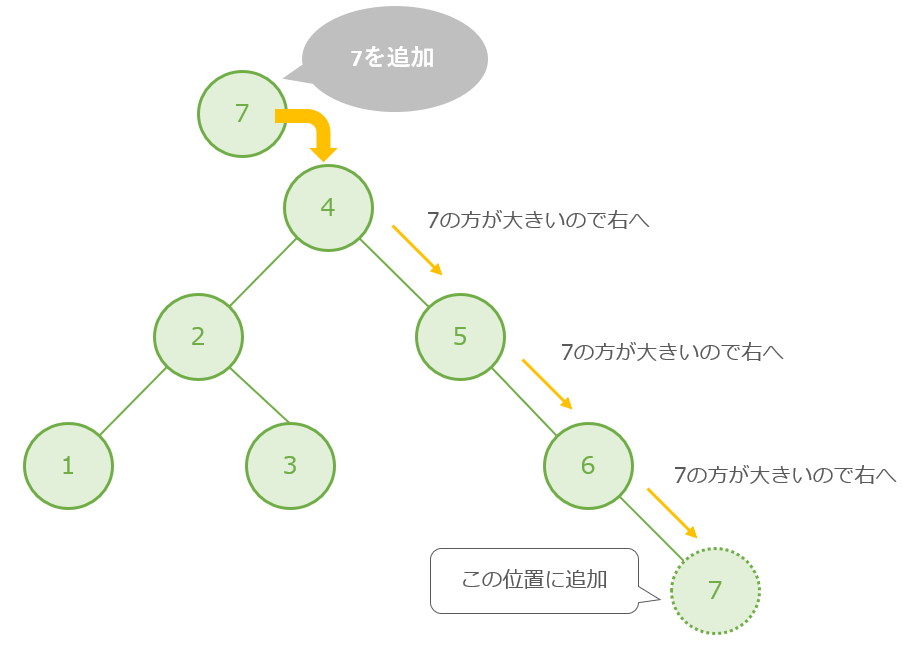
追加の流れ
- 「7」とルート「4」を比較し「7」の方が大きいので右へ
- 「7」とノード「5」を比較し「7」の方が大きいので右へ
- 「7」とノード「6」を比較し「7」の方が大きいので右へ
- 比較対象がなくなったので「7」を追加
二分探索木からデータを削除する
二分探索木からデータを削除する場合は、データを探索する場合と同じでルートから順に比較していき、追加要素の方が小さければ左へ、追加要素の方が大きければ右へ移動し削除対象のデータを探索して削除します。
ここで削除するノードが子を持っているかで動きが変わります。
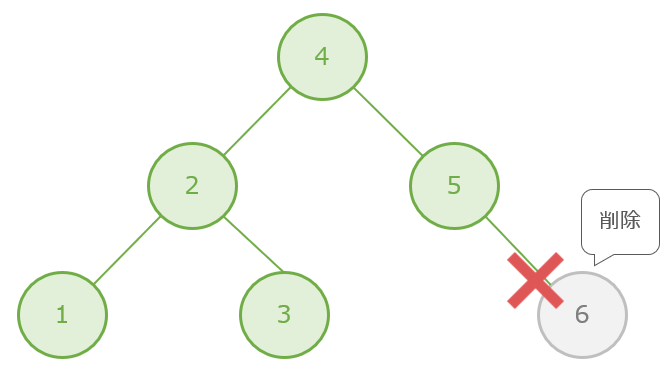
削除対象のノードが子を持っていない場合
削除対象のノードが子を持っていない場合は、ノードをそのまま削除します。
削除対象のノードが子を1つ持っている場合
削除対象のノードが子を1つ持っている場合は、削除対象ノードを削除して子ノードと位置を入れ替えます。
例えば、次の二分探索木から「5」を削除します(削除対象のノード「5」には子ノードが1つある)
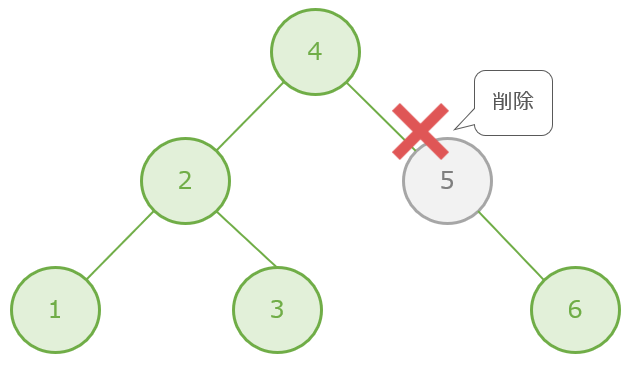
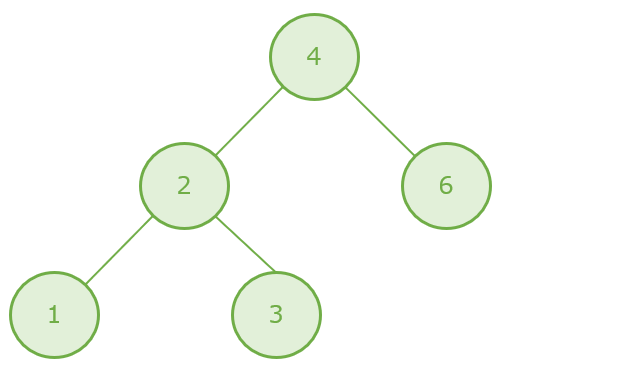
この場合は、削除対象のノード「5」は削除して、子ノード「6」をノード「5」の位置に移動します。
削除対象のノードが子を2つ持っている場合
削除対象のノードが子を2つ持っている場合は、削除対象ノードの左の子から最大値(もしくは右の子から最小値)を探索し、削除対象ノードの位置に移動します。
例えば、次の二分探索木から「4」を削除します(削除対象のノード「4」には子ノードが2つある)
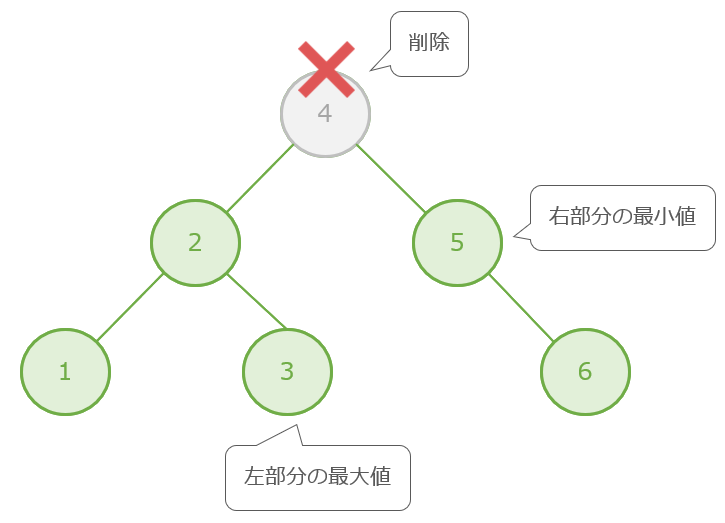
この場合は、削除対象ノードの左の子の中から最大値(ノード「3」) もしくは 右の子の中から最小値(ノード「5」)を探索し、削除対象ノードの位置に移動します。今回の例では左の子の最大値である「3」を削除対象ノードの位置に移動しています。