二分探索とは

二分探索

二分探索（にぶんたんさく）とは、探索アルゴリズムの1つです。

配列やリストのような複数のデータが格納されている箱の中から、目的のデータを探し出すのが探索であり、この探索の代表的なアルゴリズムには「線形探索」「二分探索」「ハッシュ法」があります。

本記事では、探索対象の配列やリストを「昇順」または「降順」に並び替えて探索する「二分探索」について紹介しています。

スポンサーリンク

二分探索の手順（データが見つかる場合の例）

二分探索は「昇順」または「降順」に並んでいる配列やリストに対して探索を行う手法です。探索対象を1/2ずつ削り落としていくので効率よく探索することができます。

今回の例では、「昇順」に並んでいる次の配列から「6」を二分探索で探索する手順を説明していきます。

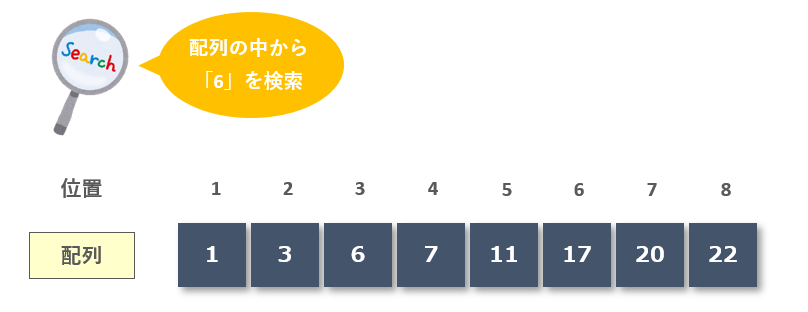
【手順1】位置1～8の真ん中のデータ「7」と比較

まずは位置1～8の中央位置を計算します。（最小位置：1、最大位置：8）

中央位置の計算方法は次の通り。

中央位置を求めると、1 + (8 - 1) / 2 = 4

配列の中央位置は4なので、位置4のデータ「7」と比較。比較した結果「６」の方が小さいので、探索の範囲を左半分に絞り込みます。

【手順2】位置1～3の真ん中のデータ「3」と比較

続いては位置1～3の中央位置を計算します。（最小位置：1、最大位置：3）

中央位置を求めると、1 + (3 - 1) / 2 = 2

配列の中央位置は2なので、位置2のデータ「3」と比較。比較した結果「６」の方が大きいので、探索の範囲を右半分に絞り込みます。

【手順3】「6」を見つけることができたので処理終了

続いては位置3のデータ「6」と比較、「6」を見つけることができたので処理終了です。

二分探索の手順（データが見つからない場合の例）

今回の例では、「昇順」に並んでいる次の配列から「18」を二分探索で探索する手順を説明していきます。

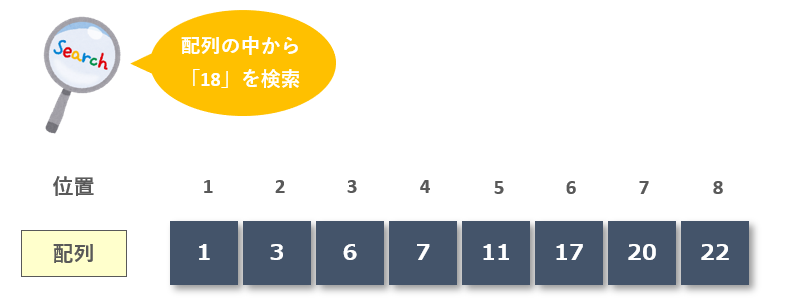
【手順1】位置1～8の真ん中のデータ「7」と比較

まずは位置1～8の中央位置を計算します。（最小位置：1、最大位置：8）

中央位置を求めると、1 + (8 - 1) / 2 = 4

配列の中央位置は4なので、位置4のデータ「7」と比較。比較した結果「18」の方が大きいので、探索の範囲を右半分に絞り込みます。

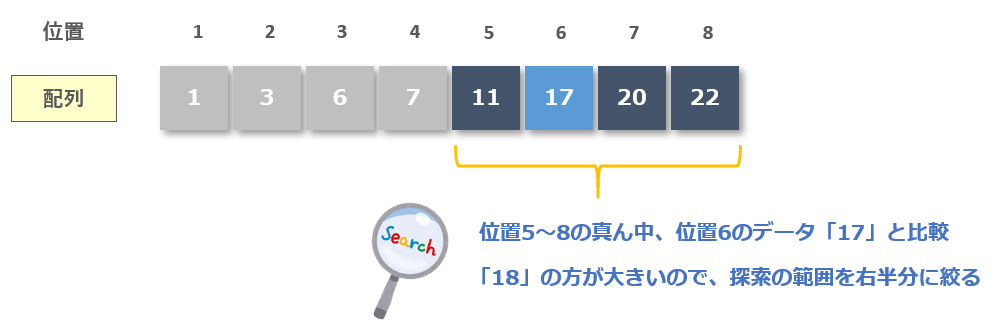
【手順2】位置5～8の真ん中のデータ「17」と比較

続いては位置5～8の中央位置を計算します。（最小位置：5、最大位置：8）

中央位置を求めると、5 + (8 - 5) / 2 = 6

配列の中央位置は6なので、位置6のデータ「17」と比較。比較した結果「18」の方が大きいので、探索の範囲を右半分に絞り込みます。

【手順3】位置7～8の真ん中のデータ「20」と比較

続いては位置7～8の中央位置を計算します。（最小位置：7、最大位置：8）

中央位置を求めると、7 + (8 - 7) / 2 = 7

配列の中央位置は7なので、位置7のデータ「20」と比較。比較した結果「18」の方が小さいので、探索の範囲を左半分に絞り込みます。

【手順4】「18」は見つからなかったので処理終了

位置7の左側はすでに確認済みのため、そこにはデータが存在しないことがわかっています。

「18」は見つからなかったので処理終了です。