目次
はじめに
基本情報技術者試験や応用情報技術者試験でよく出題される整列アルゴリズムの問題。
基本的な整列アルゴリズムには「バブルソート」「選択ソート」「挿入ソート」があり、より高速な整列アルゴリズムには「シェルソート」「クイックソート」「ヒープソート」「マージソート」があります。
本記事では、未整列データを木構造を利用してソートしていく「ヒープソート」について図解で分かりやすく解説していきます。
ヒープソートとは
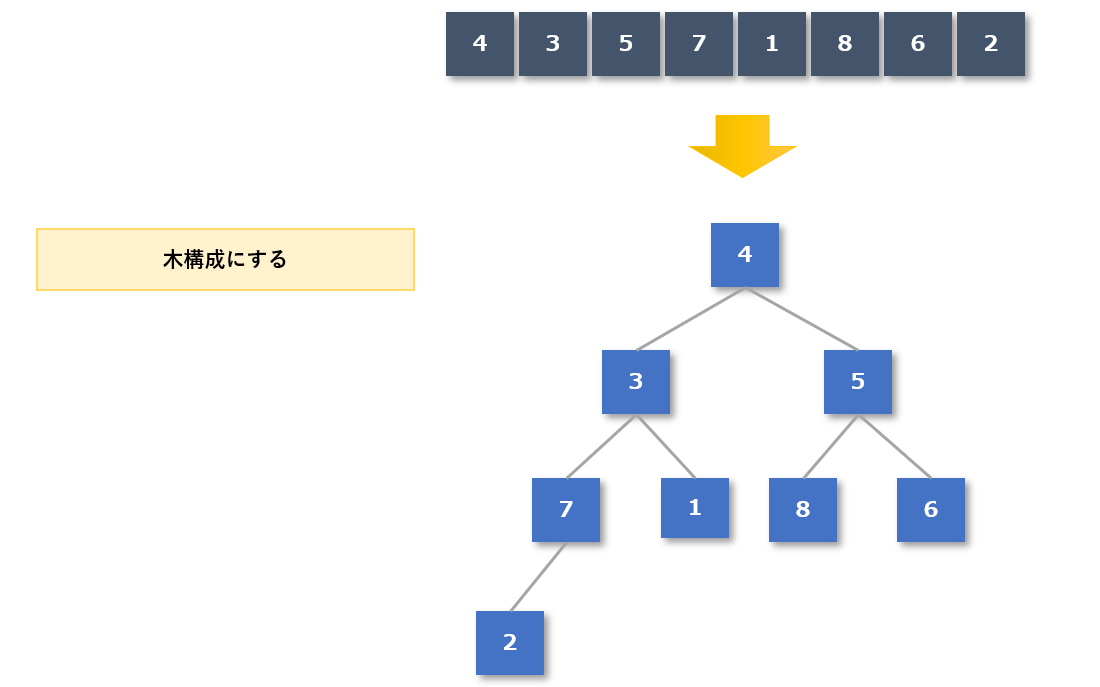
ヒープソートとは未整列のデータを「ヒープ」の性質を持つ木構造の構成にして、そこから最大値または最小値を取り出して整列、これを繰り返すことで全体を整列させる手法です。
ヒープソートの流れ
- 未整列の配列からヒープの性質を持つ木構造を作成する
- 木構造の作成が完了したら、根（ルート）の値を整列済みとする
- 根（ルート）の値を除いて、再度ヒープの性質を持つ木構造を作る
- すべてのデータが整列済みになるまで、手順2～3を繰り返す
暗記ポイント
ヒープソートとは、木構造を利用して並び替えを行う整列アルゴリズム
スポンサーリンク
【手順1】未整列の配列からヒープの性質を持つ木構造を作成する
未整列データをヒープの性質を持つ木構造を作成します（「親 ≧ 子」となるように並び替える）
まずは一番下の葉から比較
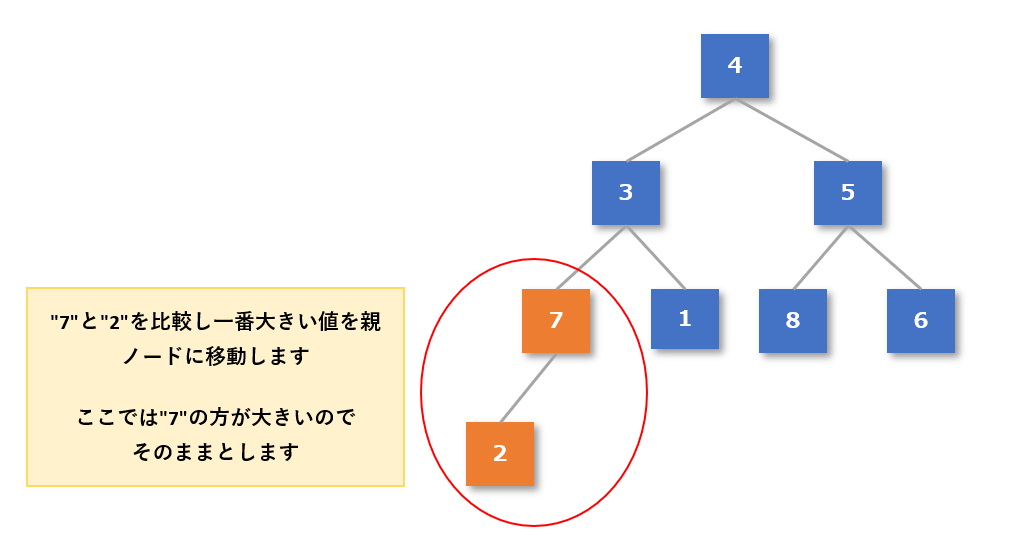
- 一番下の葉である子「2」と親「7」が「親 ≧ 子」になっているか確認する
- ここでは親「7」の方が大きいのでそのままとする
次に上のグループを比較
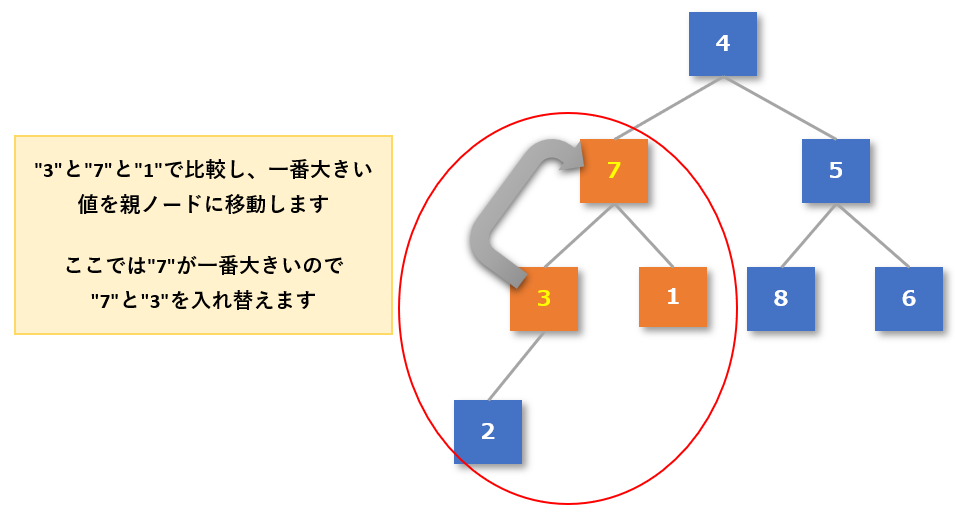
- 次に一つ上のグループである親「3」と子「7」「1」が「親 ≧ 子」になっているか確認する
- 3つの中では「7」が一番大きい数値なので、「3」と「7」を入れ替える
- 「3」が移動してきたグループが「親 ≧ 子」になっているか確認する
- 親「3」、子「2」と「親 ≧ 子」になっているのそのままとする
次に隣のグループを比較
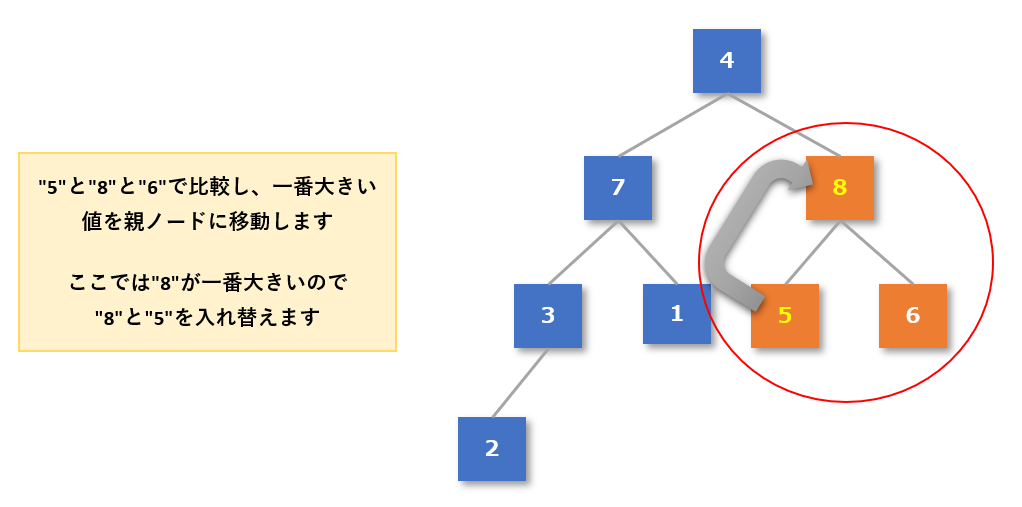
- 次に隣のグループである親「5」と子「8」「6」が「親 ≧ 子」になっているか確認する
- 3つの中では「8」が一番大きい数値なので、「5」と「8」を入れ替える
次に一番上のグループを比較
- 次に一番上のグループである親「4」と子「7」「8」が「親 ≧ 子」になっているか確認する
- 3つの中では「8」が一番大きい数値なので、「4」と「8」を入れ替える
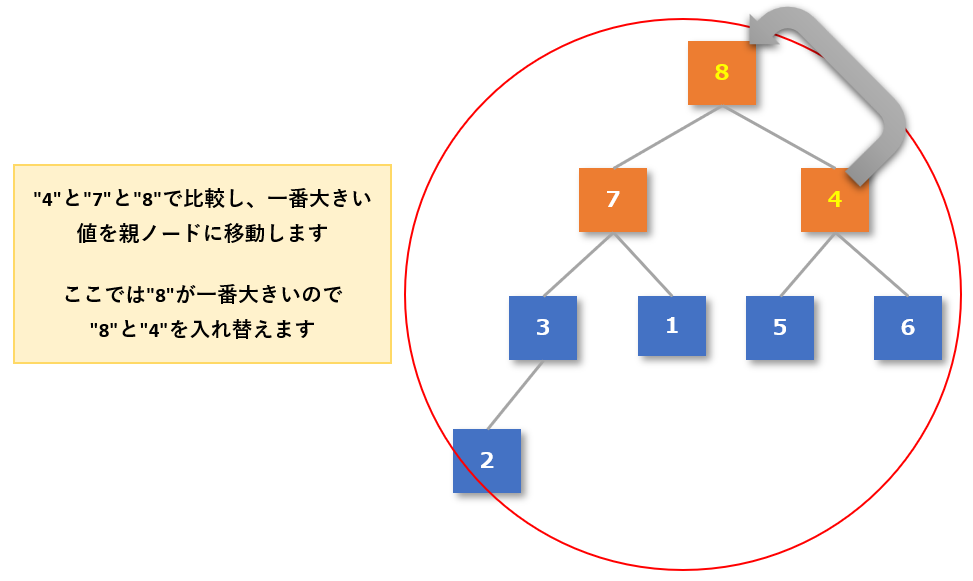
- 「4」が移動してきた右下のグループが「親 ≧ 子」になっているか確認する
- 3つの中では「6」が一番大きい数値なので、「4」と「6」を入れ替える
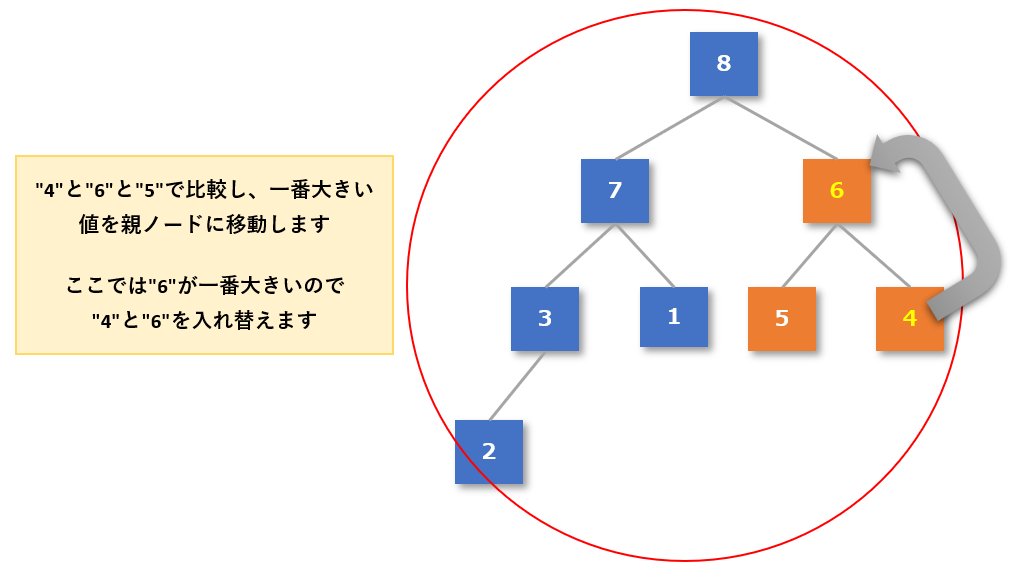
【手順2】木構造の作成が完了したら、根（ルート）の値を整列済みとする
木構造の作成が完了した（一番上の根（ルート）が最大値になった）ので、整列済みデータに最大値の「8」を追加します。
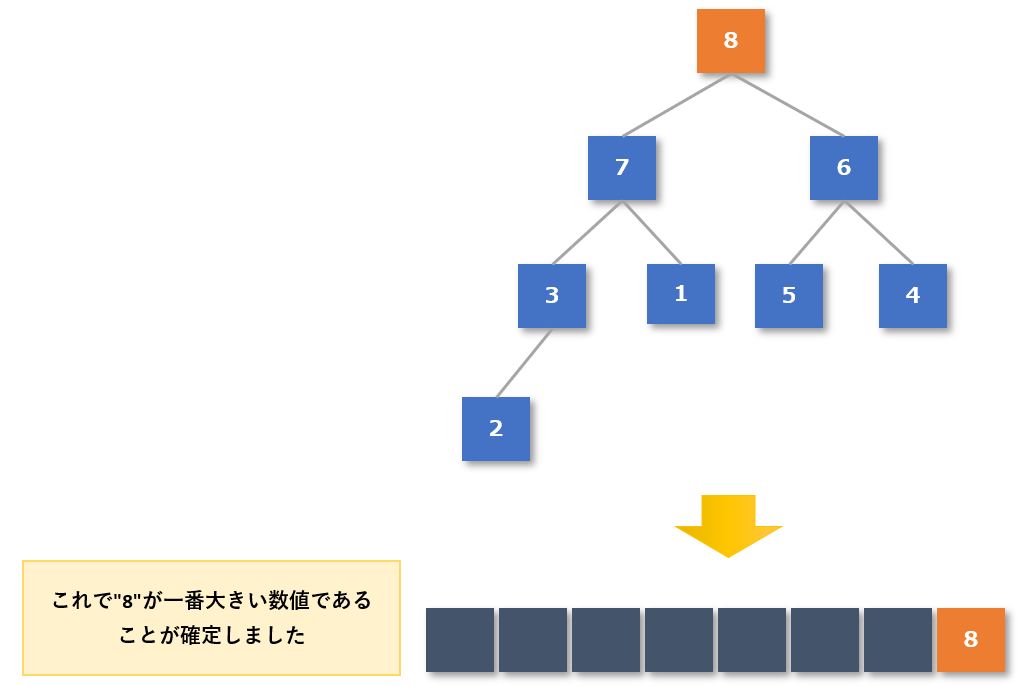
【手順3】根（ルート）の値を除いて、再度ヒープの性質を持つ木構造を作る
整列済みデータとなった「8」を除いた未整列データで再び木構成を作ります。
この時、一番下の「2」を一番上に持っていきます。
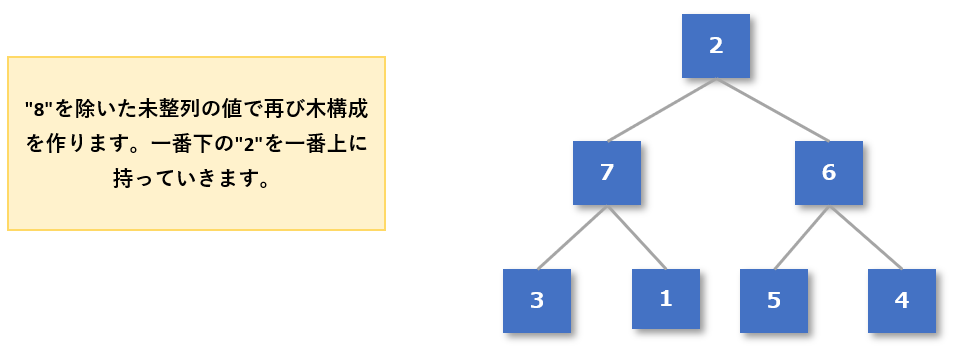
一番上のグループを比較
「2」を一番下から一番上の根（ルート）に持ってきたため、「親 ≧ 子」になっている保証がありません。そのため、一番上のグループを比較します。
（根に移動してきた「2」以外は「親 ≧ 子」になっているので「2」の部分を整列していく）
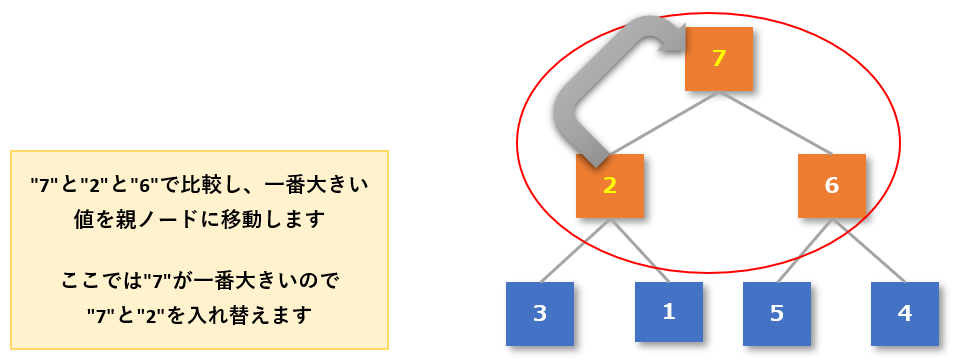
- 一番上のグループである親「2」と子「7」「6」が「親 ≧ 子」になっているか確認する
- 3つの中では「7」が一番大きい数値なので、「7」と「2」を入れ替える
左下のグループを比較
「2」が移動してきた左下のグループは「親 ≧ 子」になっている保証がないため、左下のグループを比較します。
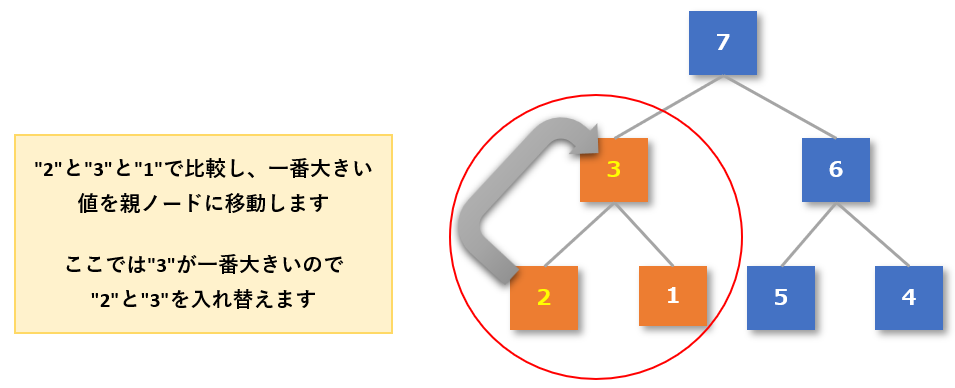
- 左下のグループである親「2」と子「3」「1」が「親 ≧ 子」になっているか確認する
- 3つの中では「3」が一番大きい数値なので、「2」と「3」を入れ替える
【手順4】すべてのデータが整列済みになるまで、手順2～3を繰り返す
【4-1手順2】木構造の作成が完了したら、根（ルート）の値を整列済みデータとする
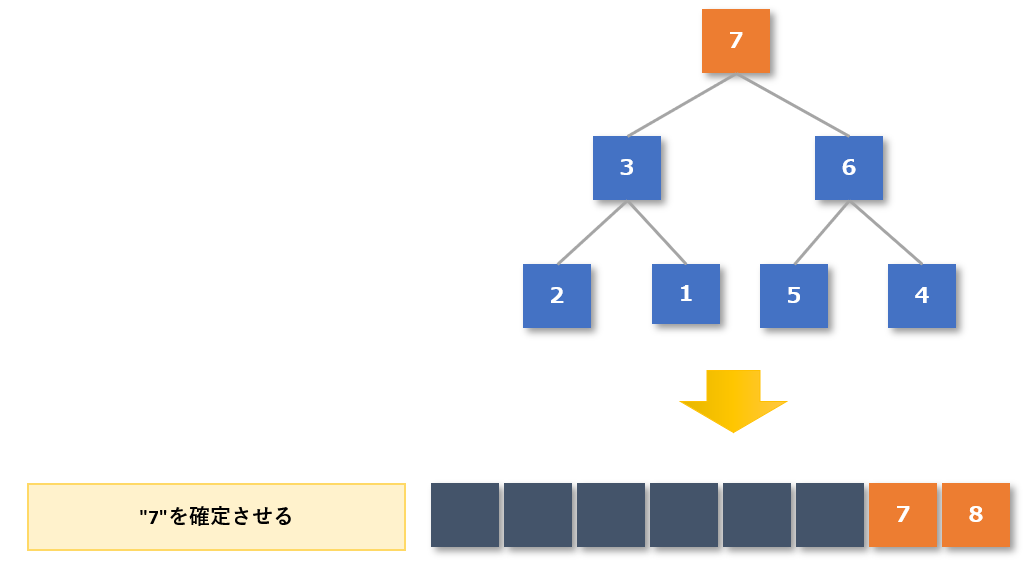
木構造の作成が完了した（一番上の根（ルート）が最大値になった）ので、整列済みデータに最大値の「7」を追加します。
【4-1手順3】根（ルート）の値を除いて、再度ヒープの性質を持つ木構造を作る
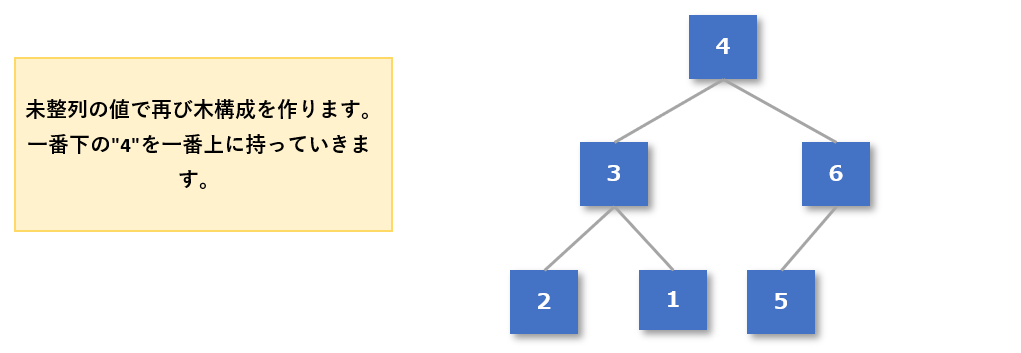
整列済みデータとなった「7」を除いた未整列データで再び木構成を作ります。
この時、一番下の「4」を一番上に持っていきます。
- 一番上のグループである親「4」と子「3」「6」が「親 ≧ 子」になっているか確認する
- 3つの中では「6」が一番大きい数値なので、「4」と「6」を入れ替える
- 「4」が移動してきた右下のグループは「親 ≧ 子」になっている保証がないため「親 ≧ 子」になっているか確認する
- 親「4」より子「5」の方が大きい数値なので、「4」と「5」を入れ替える
【4-2手順2】木構造の作成が完了したら、根（ルート）の値を整列済みデータとする
木構造の作成が完了した（一番上の根（ルート）が最大値になった）ので、整列済みデータに最大値の「6」を追加します。
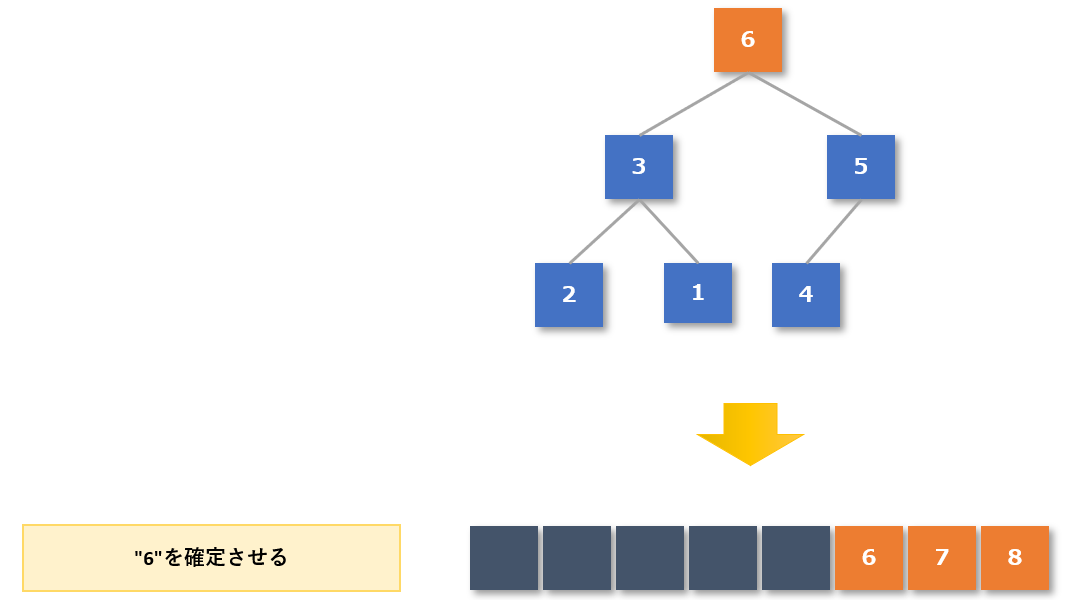
【4-2手順3】根（ルート）の値を除いて、再度ヒープの性質を持つ木構造を作る
- 整列済みデータとなった「6」を除いた未整列データで再び木構成を作る（一番下の「4」を一番上に移動する）
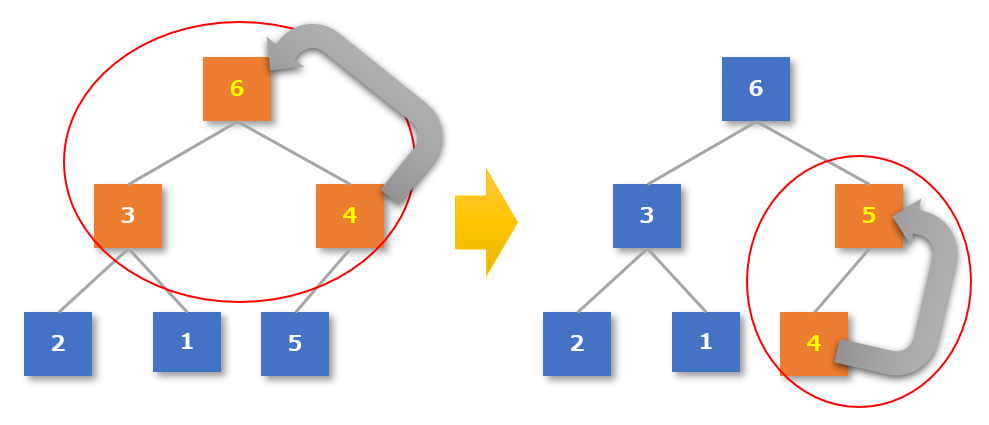
- 一番上のグループである親「4」と子「3」「5」が「親 ≧ 子」になっているか確認する
- 3つの中では「5」が一番大きい数値なので、「4」と「5」を入れ替える
【4-3手順2】木構造の作成が完了したら、根（ルート）の値を整列済みデータとする
木構造の作成が完了した（一番上の根（ルート）が最大値になった）ので、整列済みデータに最大値の「5」を追加します。
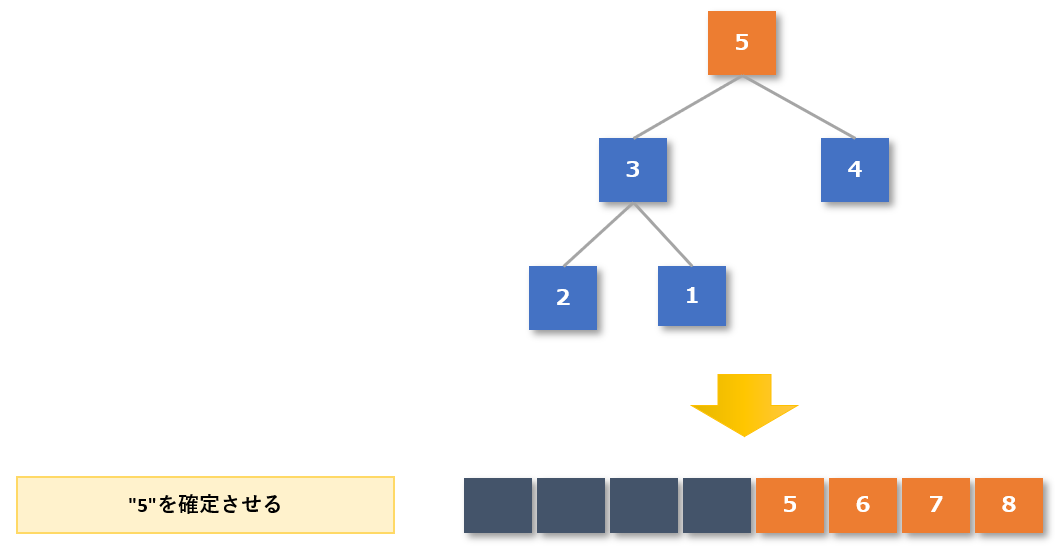
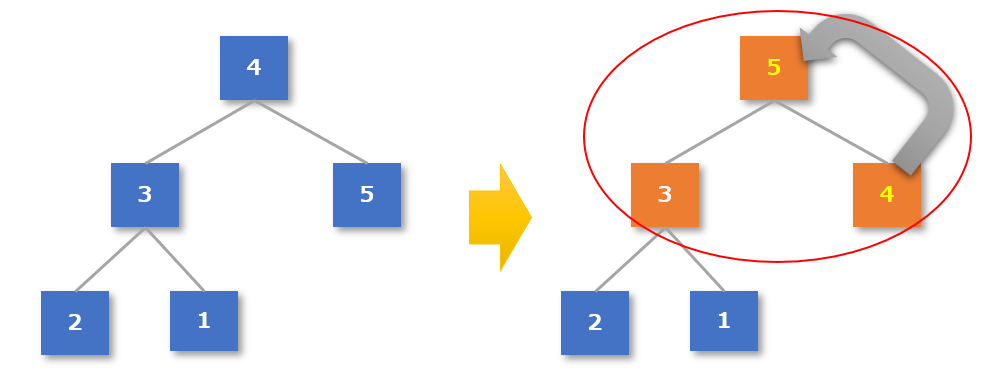
【4-3手順3】根（ルート）の値を除いて、再度ヒープの性質を持つ木構造を作る
- 整列済みデータとなった「5」を除いた未整列データで再び木構成を作る（一番下の「1」を一番上に持ってくる）
- 一番上のグループである親「1」と子「3」「4」が「親 ≧ 子」になっているか確認する
- 3つの中では「4」が一番大きい数値なので、「1」と「4」を入れ替える
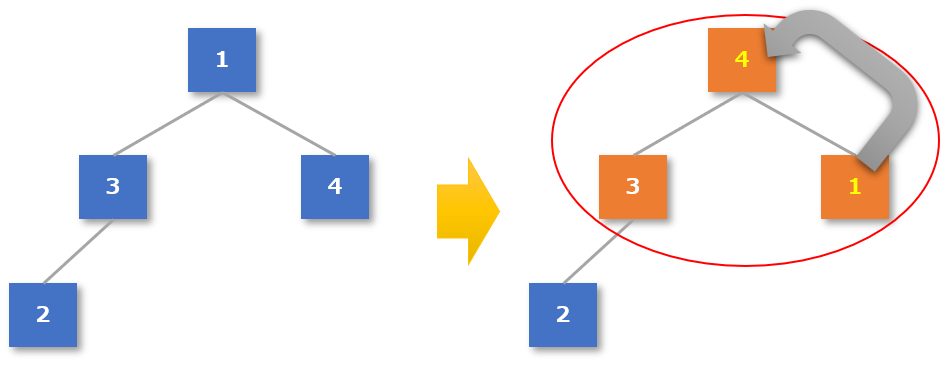
【4-4手順2】木構造の作成が完了したら、根（ルート）の値を整列済みデータとする
木構造の作成が完了した（一番上の根（ルート）が最大値になった）ので、整列済みデータに最大値の「4」を追加します。
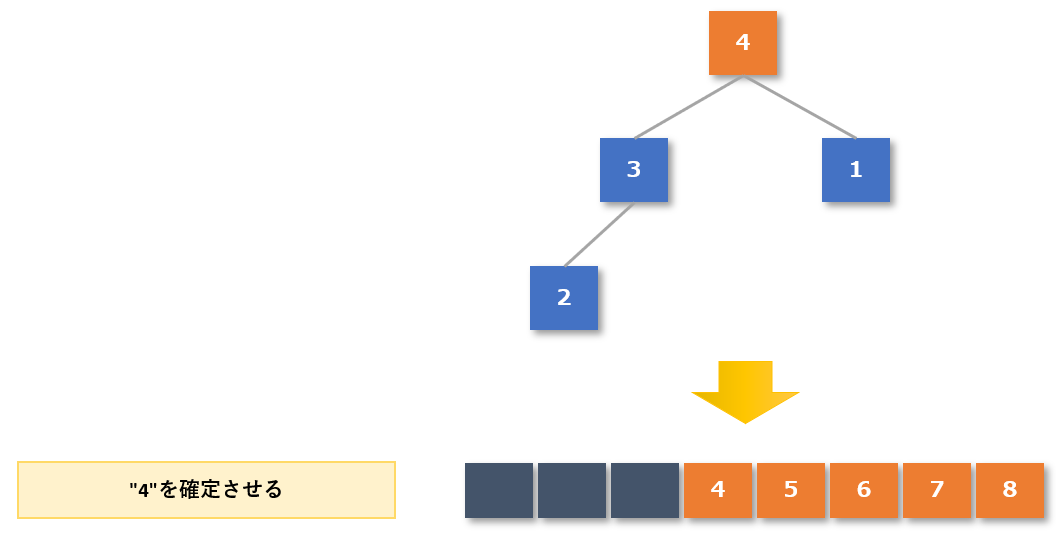
【4-4手順3】根（ルート）の値を除いて、再度ヒープの性質を持つ木構造を作る
- 整列済みデータとなった「4」を除いた未整列データで再び木構成を作る（一番下の「2」を一番上に持ってくる）
- 一番上のグループである親「2」と子「3」「1」が「親 ≧ 子」になっているか確認する
- 3つの中では「3」が一番大きい数値なので、「2」と「3」を入れ替える
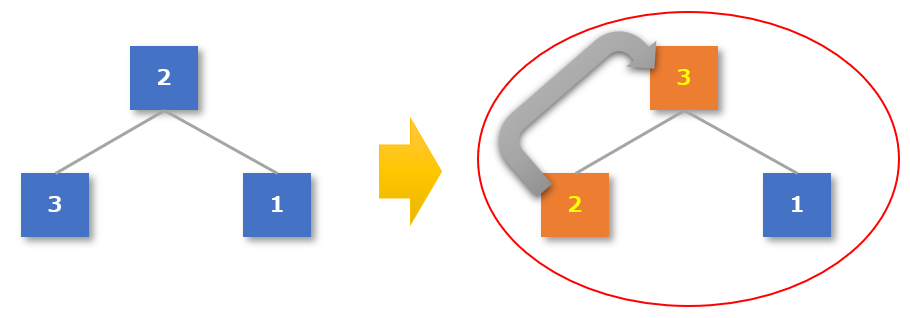
【4-5手順2】木構造の作成が完了したら、根（ルート）の値を整列済みデータとする
木構造の作成が完了した（一番上の根（ルート）が最大値になった）ので、整列済みデータに最大値の「3」を追加します。
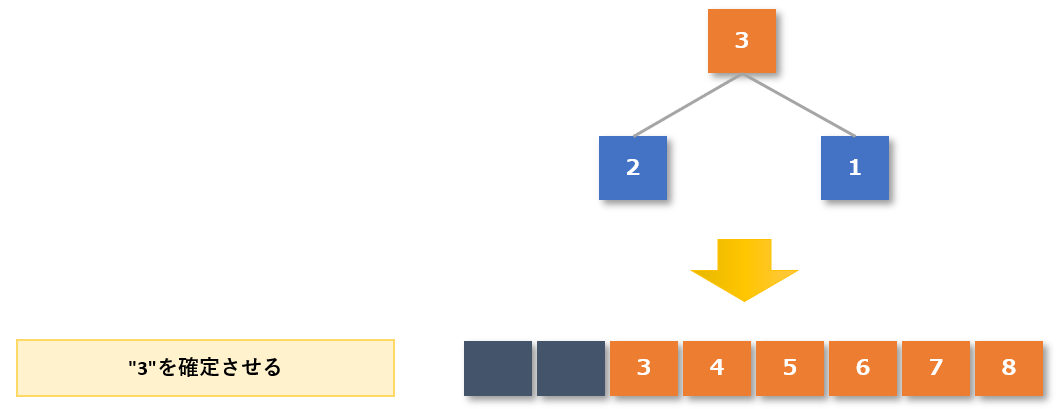
【4-5手順3】根（ルート）の値を除いて、再度ヒープの性質を持つ木構造を作る
- 整列済みデータとなった「3」を除いた未整列データで再び木構成を作る（一番下の「1」を一番上に持ってくる）
- 一番上のグループである親「1」と子「2」が「親 ≧ 子」になっているか確認する
- 親「1」より子「2」の方が大きいので、「1」と「2」を入れ替える
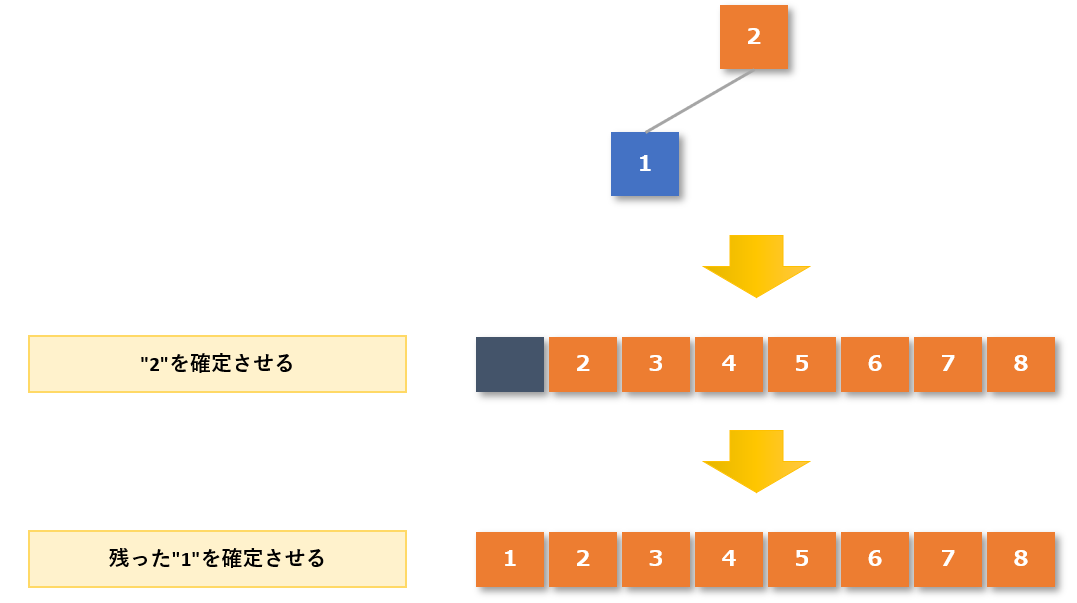
【4-6手順2】木構造の作成が完了したら、根（ルート）の値を整列済みデータとする
木構造の作成が完了した（一番上の根（ルート）が最大値になった）ので、整列済みデータに最大値の「2」を追加します。
そして、最後に残った「1」を整列済みデータに追加すれば完了です。
[基本整列アルゴリズム]
[高速整列アルゴリズム]