カルノー図法とは

カルノー図法

カルノー図とは、論理式を簡略化するための表のことです。そして、この表を用いて論理式の簡略化を行う手法のことをカルノー図法といいます。

論理式を簡略化するための表？どういうことですか？

そうですよね、それではもう少し具体的に説明していきます。

カルノー図法を利用すると、論理式を簡略化することができます。

例えば次のような論理式「A・B + A・B + A・B」があるとします。

この論理式に対してカルノー図法を用いて簡略化すると「A・B」で済むことが分かります。

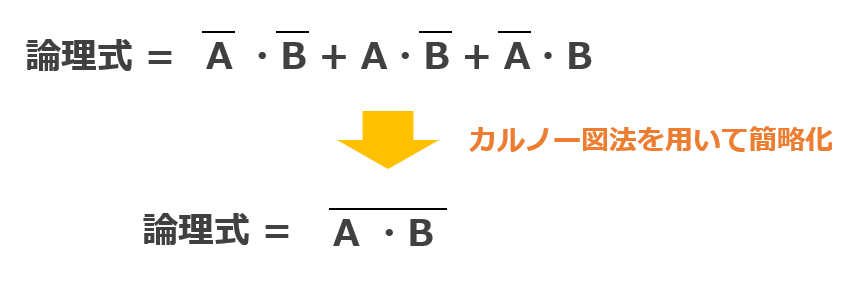
このようにカルノー図法を利用することで、論理式を簡略化することができます。

ここからは、カルノー図法の手順を解説していきます。

スポンサーリンク

カルノー図の作り方

今回の例では、論理式「A・B + A・B + A・B」のカルノー図を作成しています。

まず次のように縦軸にA、横軸にBの取り得る真偽値を書いた表を用意します。

そして、論理式「A・B + A・B + A・B」を解いていきます。

• 「A = 0」「B = 0」の場合：1
• 「A = 1」「B = 0」の場合：1
• 「A = 0」「B = 1」の場合：1
• 「A = 1」「B = 1」の場合：0

論理式を解いたらその結果をカルノー図へと反映します。

これでカルノー図の作成は完了です。

カルノー図法を用いた論理式の簡略化

続いては、カルノー図法から論理式を導き出す方法について紹介します。

手順1. グループ化する

カルノー図の中で真となる値を、長方形または正方形でグループ化します。今回の例では2つのグループが作成できます。

■グループ1

■グループ2

手順2. 共通項を導き出す

続いては各グループの、共通項を導き出します。

■グループ1

• Aが0、Bが0 → A・B
• Aが0、Bが1 → A・B

どちらも「A」が含まれているので、共通項は「A」です。

■グループ2

• Aが0、Bが0 → A・B
• Aが1、Bが0 → A・B

どちらも「B」が含まれているので、共通項は「B」です。

手順3. 共通項を論理和でくっつける

最後に共通項を論理和でくっつけます。

A + B

↓ ド・モルガンの法則

A・B

これでカルノー図法を用いた論理式の簡略化は完了です。

カルノー図法の問題例

応用情報技術者試験の過去問を用いて、カルノー図法の問題を解いていきます。

A，B，C，Dを論理変数とするとき，次のカルノー図と等価な論理式はどれか。ここで，・は論理積，＋は論理和，XはXの否定を表す。

ABCD	00	01	11	10
00	1	0	0	1
01	0	1	1	0
11	0	1	1	0
10	0	0	0	0

ア：  A・B・C・D + B・D

イ：  A・B・C・D + B・D

ウ：  A・B・D + B・D

エ：  A・B・D + B・D

出典：応用情報技術者試験平成26年度秋期 午前問1

グループ化

まずはカルノー図の真の値をグループ分けします。

■グループ1

※上下と左右の端はつながっていると考えてグループ化します。

■グループ2

共通項を導き出す

■グループ1

• Aが「0」、Bが「0」、Cが「0」、Dが「0」→ A・B・C・D
• Aが「0」、Bが「0」、Cが「1」、Dが「0」→ A・B・C・D

共通項は「A・B・D」

■グループ2

• Aが「0」、Bが「1」、Cが「0」、Dが「1」→ A・B・C・D
• Aが「0」、Bが「1」、Cが「1」、Dが「1」→ A・B・C・D
• Aが「1」、Bが「1」、Cが「0」、Dが「1」→ A・B・C・D
• Aが「1」、Bが「1」、Cが「1」、Dが「1」→ A・B・C・D

共通項は「B・D」

共通項の論理和

最後に共通項を論理和でくっつけると「A・B・D + B・D」となり、答えは「エ」です。