補数とは
補数とは「補う数」という意味で、「基数の補数」と「減基数の補数」という2種類の補数が存在します。
基数の補数
基数の補数とは「足すと桁が1つ上がる数のうち最も小さい数」のことです。
例えば、10進数の「4」という数に「6」を足すと、桁が1つ上がり「10」となり、「6」は10進数における「4」に対する「10の補数」といいます。
2進数では「2の補数」といい、コンピュータでは負の数をあらわすために使われています。
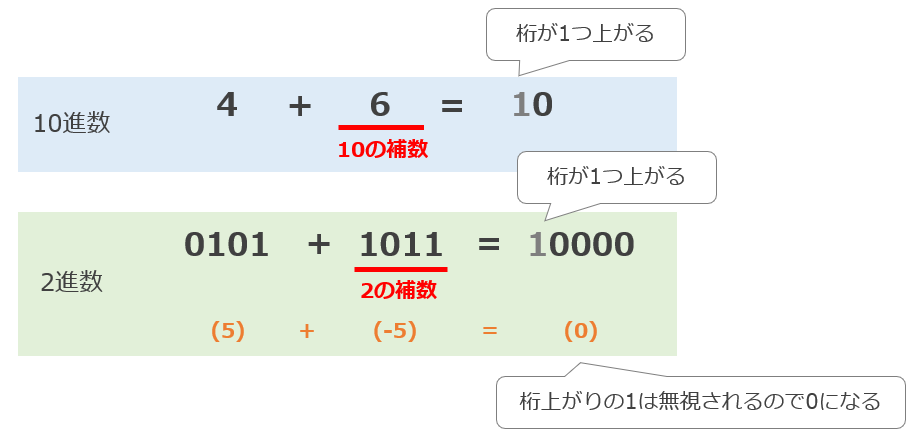
基数の補数は次のように求めることができます。
[10進数の例] 4の10の補数を求める
10 - 4 = 6 ← これが10の補数
[2進数の例] 0101の2の補数を求める
10000 - 0101 = 1011 ← これが2の補数
スポンサーリンク
減基数の補数
減基数の補数とは「足しても桁上がりしない数のうち最も大きい数」のことです。
例えば、10進数の「4」という数に「5」を足すと、桁内の最大値「9」となり、「5」は10進数における「4」に対する「9の補数」といいます。(2進数では「1の補数」)
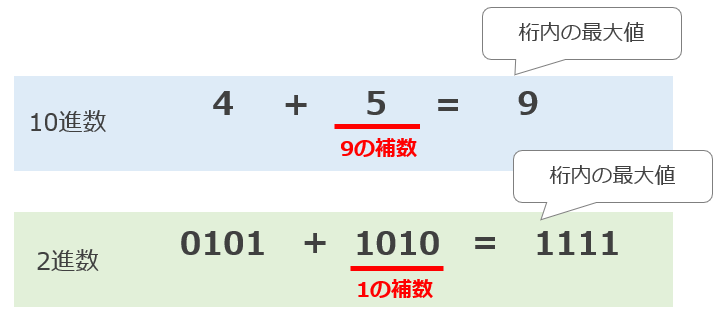
減基数の補数は次のように求めることができます。
[10進数の例] 4の9の補数を求める
9 - 4 = 5 ← これが9の補数
[2進数の例] 0101の1の補数を求める
1111 - 0101 = 1010 ← これが1の補数
2の補数とは
2の補数とは、上記で説明した基数(2進数)の補数(足すと桁が1つ上がる数のうち最も小さい数)のことです。
2の補数の求め方
2の補数の求め方は2通りあります。
1つは次のような式で求めることができます。
[例] 0101の2の補数を求める
10000 - 0101 = 1011 ← これが2の補数
そして、もう一つは次のようにすることで簡単に求めることができます。
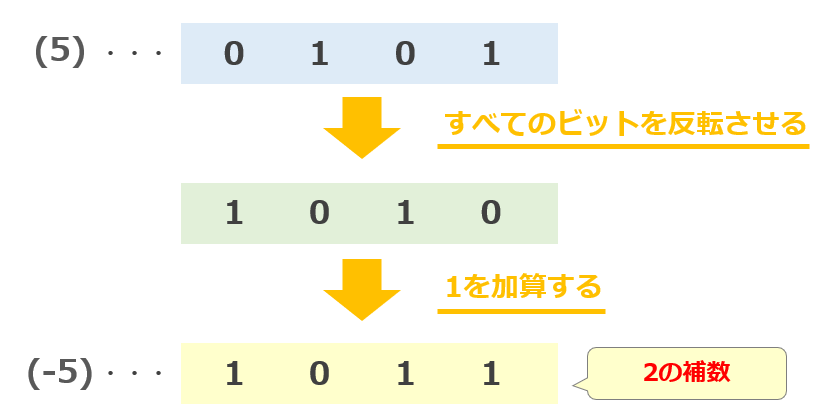
手順1. すべてのビットを反転させる。※[例] 0101(5)の2の補数を求める
0101
↓ すべてのビットを反転させる
1010
手順2. 反転させたビットに1を加算する。
1010 + 0001 = 1011(-5)← 0101(5)の2の補数
2の補数は最上位ビットを符号として扱うことができ、最上位ビットが「0」の場合は「正の数」、「1」の場合は「負の数」をあらわしています。
この正の数と負の数はお互いに2の補数という関係にあります。※例えば、正の数「0100(4)」の2の補数は負の数「1100(-4)」であり、負の数「1100(-4)」の2の補数は正の数「0100(4)」となる。
1の補数とは
1の補数とは、上記で説明した減基数(2進数)の補数(足しても桁上がりしない数のうち最も大きい数)のことです。
1の補数の求め方
1の補数の求め方は2通りあります。
1つは次のような式で求めることができます。
[例] 0101の1の補数を求める
1111 - 0101 = 1010 ← これが1の補数
そして、もう一つはすべてのビットを反転させることで簡単に求めることができます。
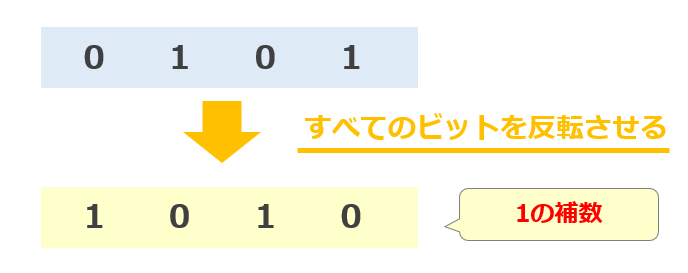
手順1. すべてのビットを反転させる。※[例] 0101の1の補数を求める
0101
↓ すべてのビットを反転させる
1010 ← 1の補数

