目次
ヒストグラム
ヒストグラムとは、収集したデータを区間ごとに区切り、その区間ごとのデータ個数を棒グラフで表したものです。ヒストグラムを作成することで、データの分布状況(バラつき)を視覚的に認識することができます。
また、ヒストグラムは 数値データなどを統計・分析して品質管理に役立てる法である「QC七つ道具」の一つです。
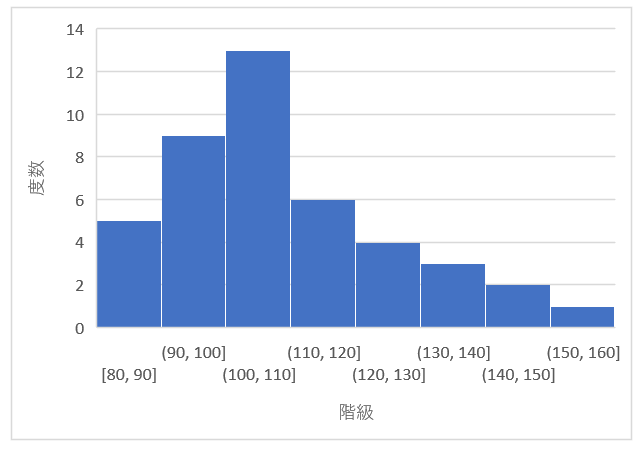
上記がヒストグラムの例です。ヒストグラムでは、縦軸を「度数」、横軸を「階級」で表現します。


ヒストグラムの作り方
スポンサーリンク
[手順1] データを収集する
まずはヒストグラムを作るためのデータを収集します。
今回は、みかんの重量を例とします。
| みかんの重量(g) | ||
| 90 | 100 | 120 |
| 89 | 121 | 130 |
| 136 | 91 | 110 |
| 101 | 105 | 115 |
| 106 | 116 | 100 |
| 113 | 102 | 100 |
| 101 | 109 | 70 |
度数分布表を作る
収集したデータから「度数分布表」を作成します。度数分布表とは下記のような表です。
階級:1つ1つの区間のこと
度数:各階級に入る個数のこと
今回の例では、10gの範囲で階級を分けています。
| 階級(重量) | 度数(個数) |
| 70g~80g | 1 |
| 81g~90g | 2 |
| 91g~100g | 4 |
| 101g~110g | 7 |
| 111g~120g | 4 |
| 121g~130g | 2 |
| 131g~140g | 1 |
ヒストグラムを作成する
最後に度数分布表からヒストグラムを作成します。
縦軸には度数(重量)、横軸(個数)には階級を入れます。作成したヒストグラムからみかんの重量は100~110gが最も多い(※あくまでもデータは例です)ことがわかります。


ヒストグラムの種類と見方
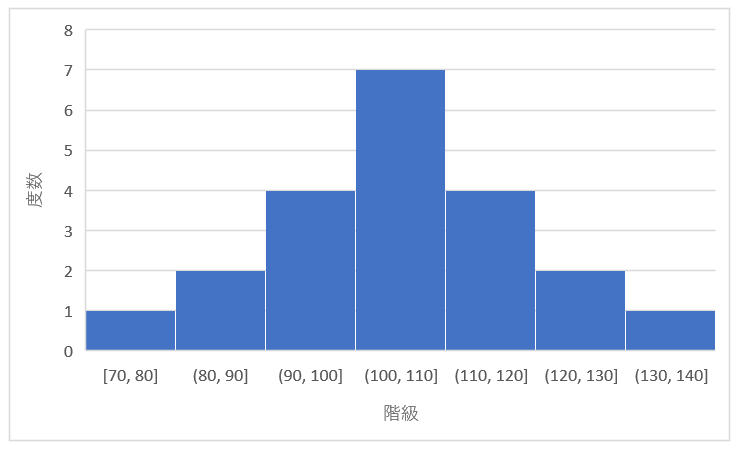
左右対称型(一般型)
中央を頂点とし、そこから左右にバラつきが見られ、中心から両端に離れるにしたがって徐々に少なくなるのが、左右対称型(一般型)です。
左右対称になるのが特徴で、安定したデータの時に見られる形です。
離れ小島型
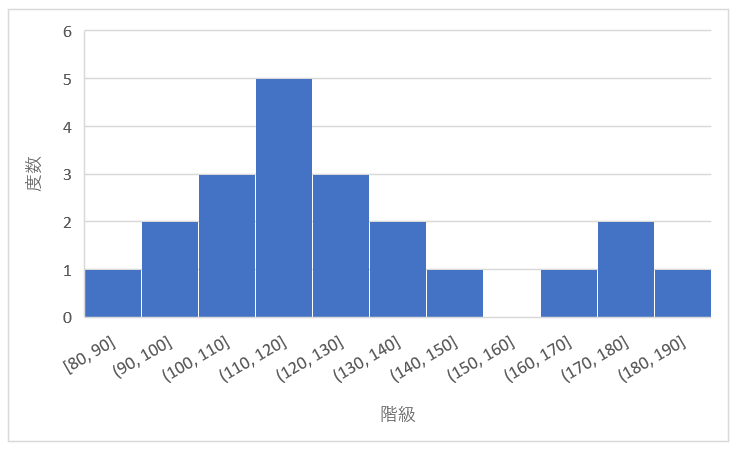
ヒストグラムの右の端、もしくは左の端に離れ小島があるのが特徴です。
本来の山とは離れた場所にあるため、測定に誤りがあった可能性が考えられます。
ふた山型
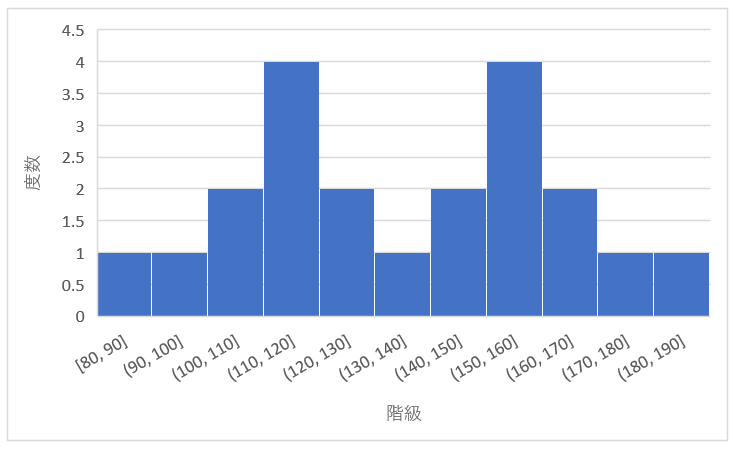
大きな山が二つできるのがふた山型の特徴です。
平均値が異なる2つの分布が混じっている可能性があります。
歯抜け型(くし歯型)
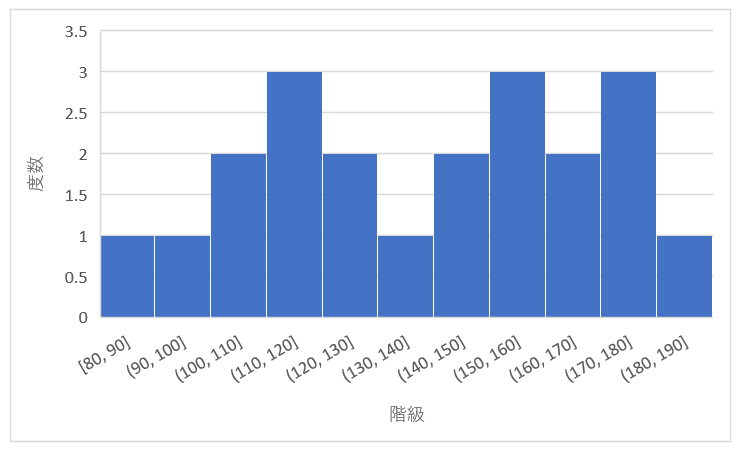
綺麗な山ではなく、デコボコした山になるのが歯抜け型の特徴です。データが少ない場合や、区間の幅(目盛)の決め方が悪い場合にこの形になることがあります。
歯抜け型の傾向が見られた場合は、データ採取方法やヒストグラムの作成方法を再検討する必要があります。
右すそ引き型(左すそ引き型)
ヒストグラムの山が中心よりも左右どちらかに寄っているのが特徴です。下限または上限に制限が設けられている場合などにみられる形です。
左絶壁型(右絶壁型)
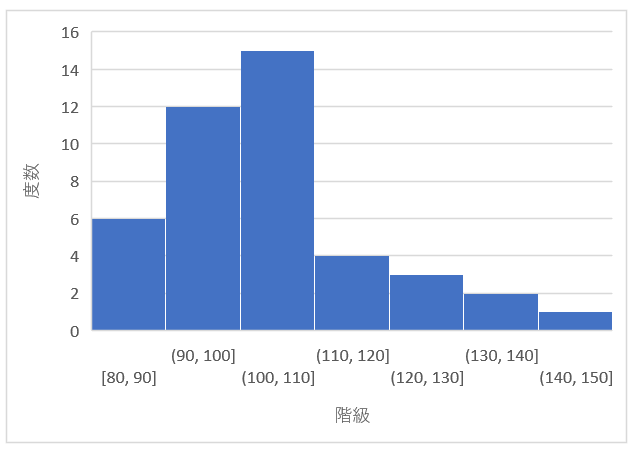
ヒストグラムの山が中心よりも極端に左右どちらかに寄っているのが特徴です。データが選別されている場合などに見れれる形です。