目次
散布図
散布図とは、2つの項目の相関関係を把握するためのグラフです。グラフ上にプロット(点を打つこと)していき、その点のばらつき具合によって2つの項目の相関関係を判断することができます。
以下が散布図のイメージ例です。
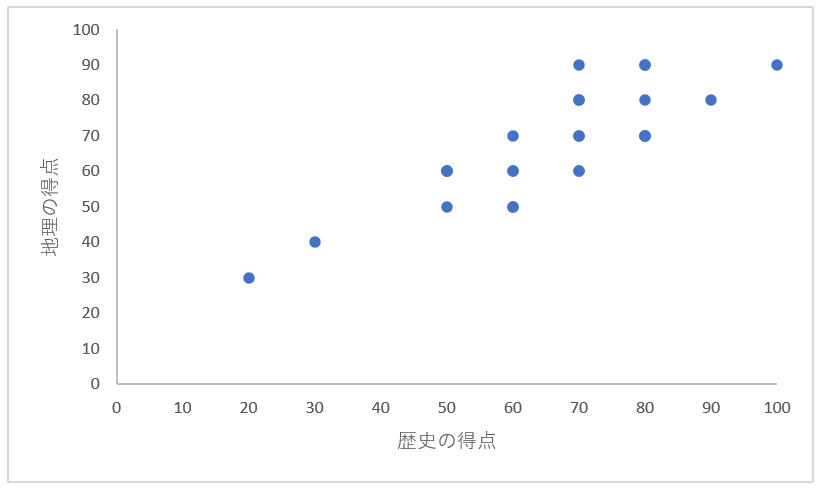

散布図は、主に数値データなどを統計してまとめ、これを分析して品質管理に役立てる手法である「QC七つ道具」の一つです。
散布図の相関関係
散布図の相関関係には「正の相関」「負の相関」「関係なし」の3パターンが存在します。
正の相関
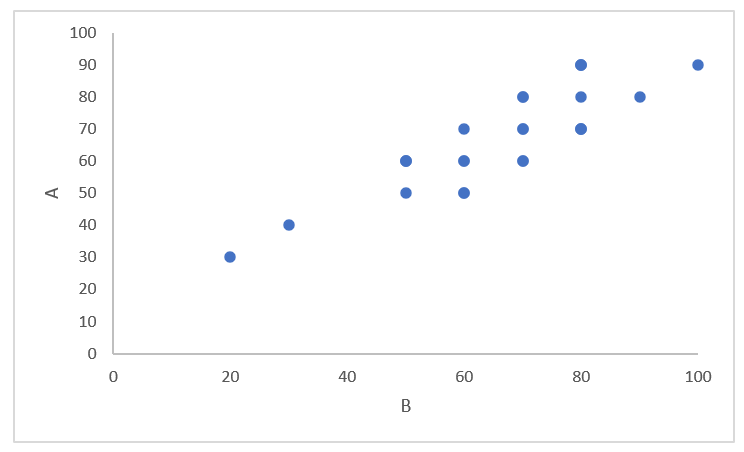
正の相関とは、Aの値が大きくなるとBの値も大きくなるという関係性を示します。
例えば、気温が温かくなると冷たい商品の売上があがる、雨の量が増えると傘の売上が上がるというような場合は、このような形が見られます。
負の相関
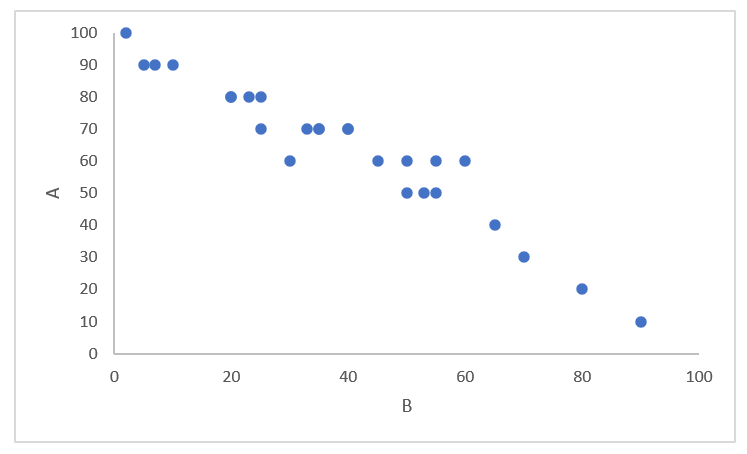
負の相関とは、Aの値が大きくなるとBの値は小さくなるという関係性を示します。
例えば、気温が低くなると温かい商品の売上が上がるというような場合は、このような形が見られます。
相関なし
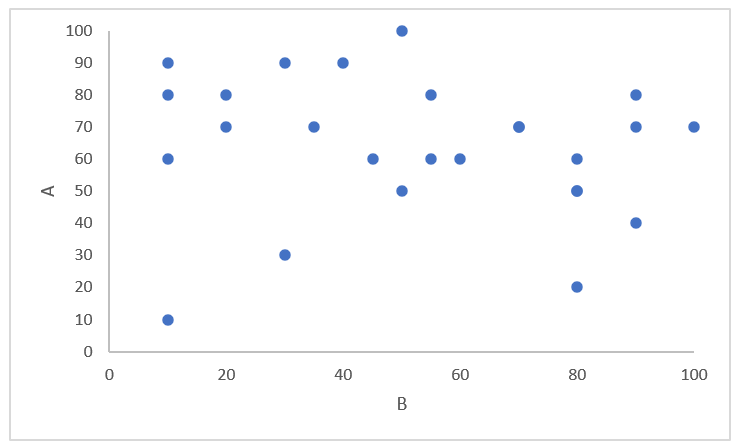
相関なしとは、AとBの値には関係性が見られないというケースです。
散布図の作り方
[手順1] 相関関係を調べるデータを用意する
まずは散布図を作成するためのデータを用意します。
今回は、歴史と地理の得点を例とします。
| 名前 | 歴史の得点 | 地理の得点 | 名前 | 歴史の得点 | 地理の得点 |
| A | 90 | 80 | J | 70 | 80 |
| B | 80 | 90 | K | 80 | 70 |
| C | 70 | 70 | L | 70 | 80 |
| D | 100 | 90 | M | 80 | 80 |
| E | 70 | 90 | N | 60 | 70 |
| F | 80 | 70 | O | 70 | 60 |
| G | 50 | 60 | P | 80 | 70 |
| H | 20 | 30 | Q | 50 | 60 |
| I | 50 | 50 | R | 60 | 60 |
[手順2] 用意したデータを使い散布図を作る
相関関係を調べるデータが用意できたら、データをグラフにしていきます。横軸を「歴史の得点」、縦軸を「地理の得点」とし、お互いの範囲を0~100にします。
そして、集めたデータを1つ1つグラフに点を打っていきます。
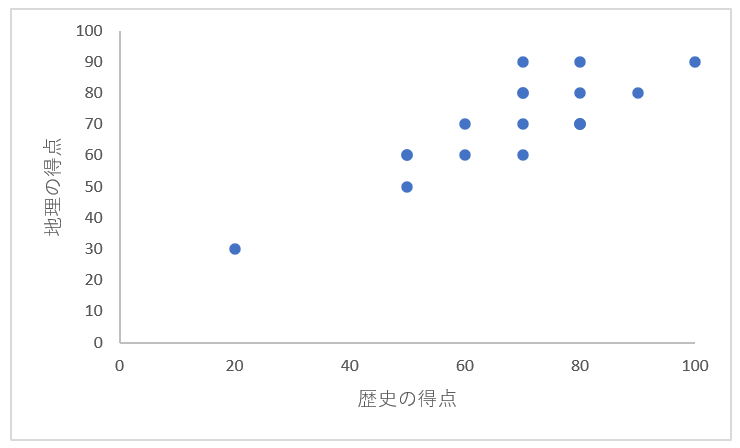

これで散布図の完成です。
完成した散布図から「正の相関」であることが分かります。
helpful
この記事は役に立ちましたか?

