基数と基数変換がわかる【基本情報技術者試験対策】

基本情報技術者試験の参考書を読むと大抵はじめに出てくる内容である「基数」と「基数変換」、2進数？16進数？と普段の生活では使わない言葉がでてくるため、ここで挫折してしまう人も多いのではないでしょうか。

本記事では「基数」と「基数変換」について図解で分かりやすく解説していきます。

基数

基数とは、数値を表現する際に位取りの基準となる数のことであり、2進数や10進数などの「n進数」のnの部分を基数といいます。

スポンサーリンク

2進数

2進数とは「0」と「1」という2個の数字であらわしたものです。

コンピュータが扱う最小単位のことをビット（bit）といい、1ビットで表現できる数字は「0」と「1」の2つだけです。この「0」と「1」という2個の数字で数をあらわすのが2進数です。

そして、コンピュータの世界では 1バイト（Byte）= 8ビット（bit）と定義されています。

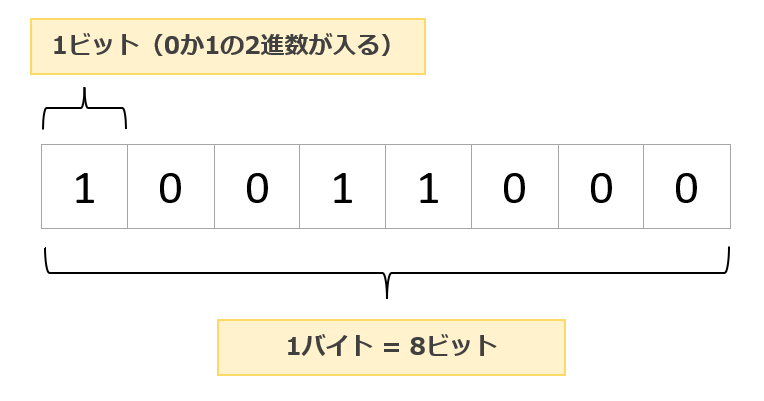
コンピュータはこの「0」と「1」の集まりしか理解できません。そのため、コンピュータでは「0」と「1」の集まりでデータを表現します。

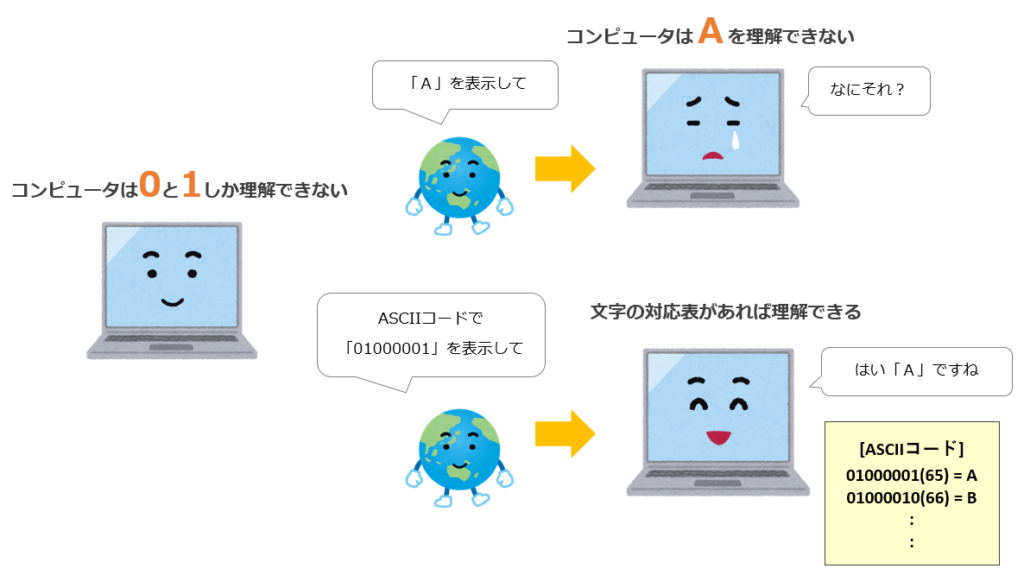
コンピュータに文字を表現させているのは「文字コード」と呼ばれるものです。

コンピュータが理解できる「0」と「1」の集まりと、文字の対応表を作り コンピュータはその対応表通りに文字を表現しています。

8進数と16進数

コンピュータの基本は2進数です。しかし「0」と「1」しか使えない表記だと、桁数が膨大になってしまいます。そこで1桁である程度まとまった区切りができ、コンピュータと相性の良いn進数表記が必要です。それが8進数と16進数です。

8進数は0～7の8通りの数で表現します。8進数の1桁は2進数の3桁（3ビット）と同じ情報量です。

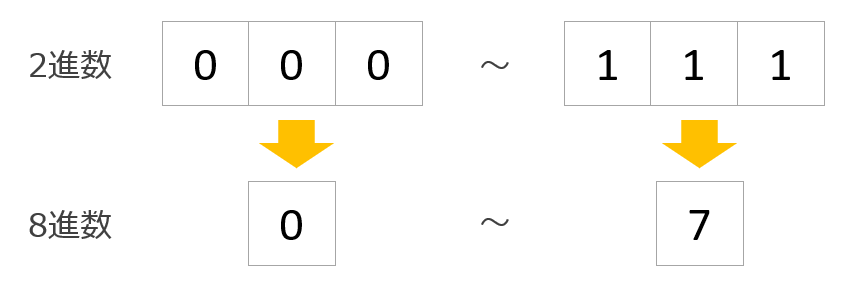
そして、16進数は0～Fの16通りの数で表現します。16進数の1桁は2進数の4桁（4ビット）と同じ情報量です。

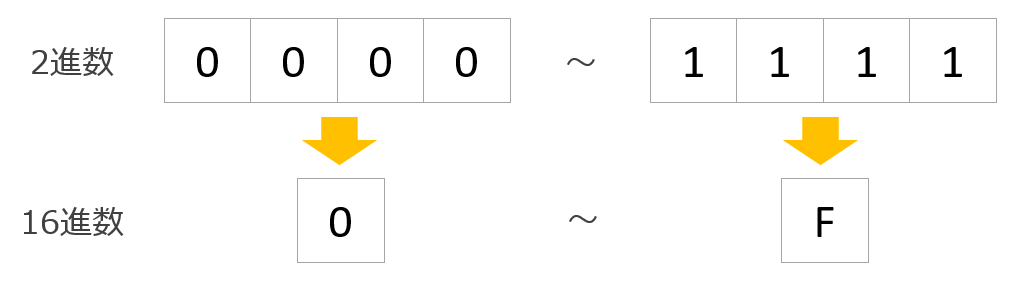
2進数と8進数、16進数の対応表は次のとおりです。

10進数	2進数	8進数	16進数
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F
16	10000	20	10

10進数

私たち人がものを数える時には、0～9という10個の数字を使います。この0～9という10個の数字で数をあらわすのが10進数です。

基数変換

スポンサーリンク

基数と桁の重み

10進数から2進数へ変換するときなどの使うのが「桁の重み」です。

桁の重みとは、各桁の単位のことで、10進数で例えると「100の位」「10の位」「1の位」など、「～の位」を桁の重みといいます。

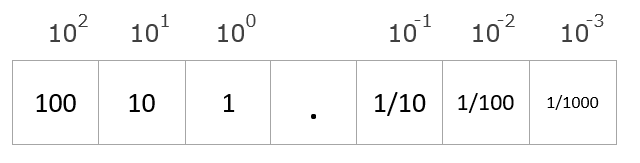
n進数の桁の重みは次の法則で決まります。(整数部3桁、小数部3桁の例）

10進数で見てみると、桁が増えるごとに10倍ずつ増えているのがわかります。

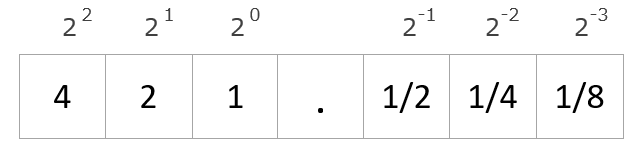
2進数、8進数、16進数も同じ考え方です。以下は2進数の桁の重みです。桁が増えるごとに2倍ずつ増えています。

n進数から10進数への基数変換

n進数を10進数に変換するには、各桁に対して「桁の重み」を掛け、それを合算することで求めることができます。

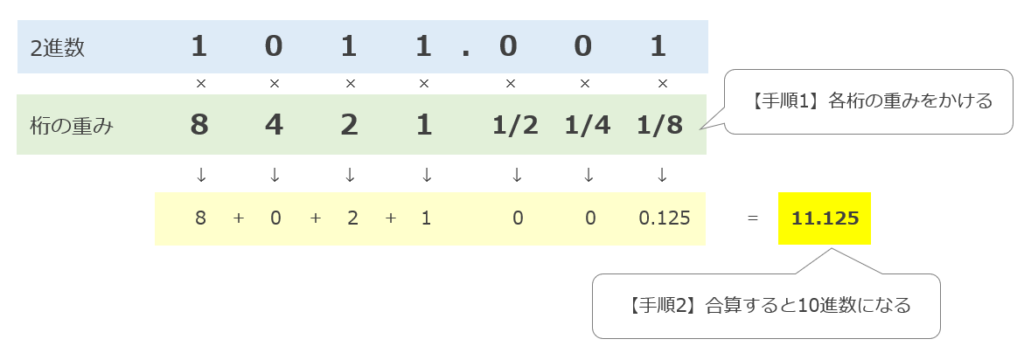
上記は2進数「1011.001」を10進数へ変換するイメージ図です。

10進数からn進数への基数変換

10進数をn進数に変換するには、次のように10進数の整数部を基数で割っていきます。（今回の例は2進数への変換なので2で割る）

続いては小数部です。次のように10進数の小数部に対して基数を掛けていきます。（今回の例は2進数への変換なので2を掛ける）

2進数から8進数への基数変換

2進数を8進数に変換するには、次の3ステップを実施します。

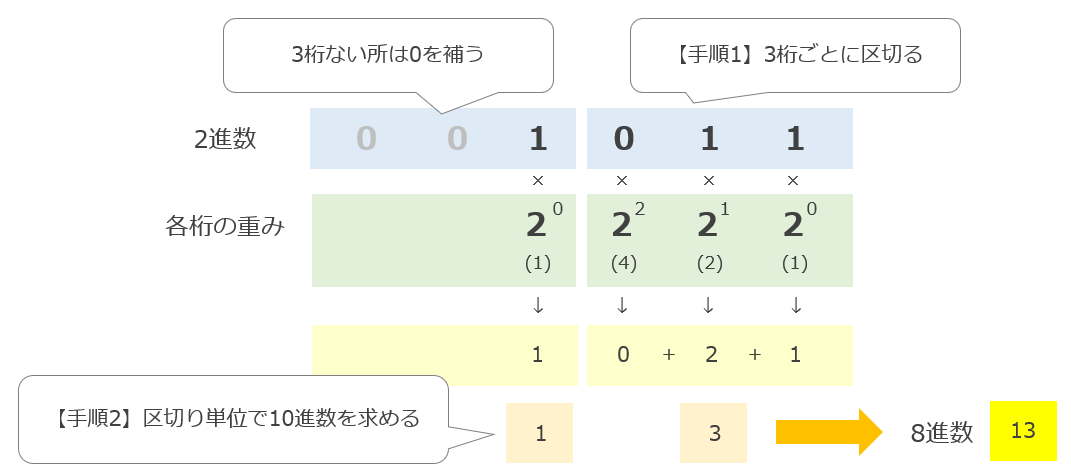
[ステップ1] 2進数を3桁ごとに区切る

[ステップ2] ステップ1で区切った、区切り単位で10進数に変換する

[ステップ3] ステップ2で求めた10進数を連結する

2進数から16進数への基数変換

2進数を16進数に変換するには、次の4ステップを実施します。

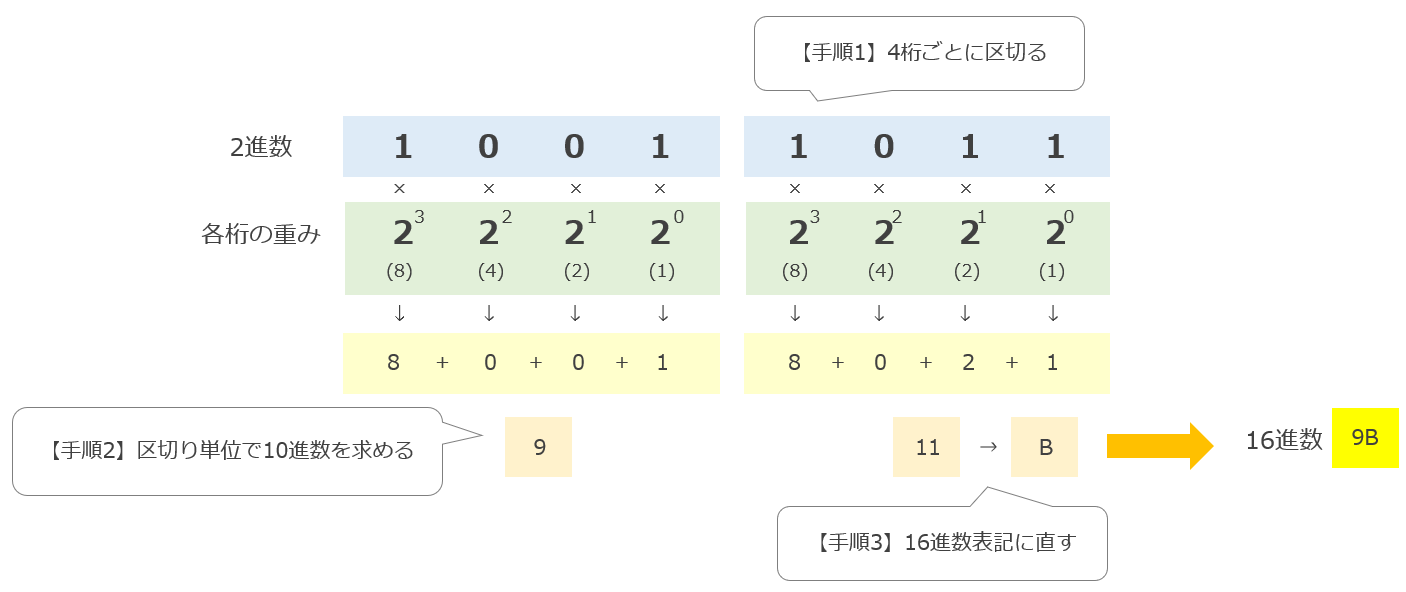
[ステップ1] 2進数を4桁ごとに区切る

[ステップ2] ステップ1で区切った、区切り単位で10進数を求める

[ステップ3] ステップ2で求めた10進数を16進数表記にする

[ステップ4] ステップ3で求めた16進数を連結する

8進数から2進数への基数変換

8進数から2進数に変換するには、次の3ステップを実施します。（2進数から8進数を求めた時と逆のことをする）

[ステップ1] 8進数をバラバラにして10進数に戻す

[ステップ2] ステップ1で求めた10進数を2進数に変換する

[ステップ3] ステップ2で求めた2進数を連結する

16進数から2進数への基数変換

16進数から2進数に変換するには、次の3ステップを実施します。（2進数から16進数を求めた時と逆のことをする）

[ステップ1] 16進数をバラバラにして10進数に戻す

[ステップ2] ステップ1で求めた10進数を2進数に変換する

[ステップ3] ステップ2で求めた2進数を連結する

スポンサーリンク

基本情報技術者試験 過去問の解説

【解き方その1】シンプルに計算する

まずは10進数で割り算を行います。

これを2進数に変換します。

【解き方その2】シフト演算を使う

シフト演算とは、2進数をあらわすビット列を左または右にずらす操作のことです。

例えば、10進数の「7」という数字を10倍（左にシフト）すると「70」、1/10倍（右にシフト）すると「0.7」です。

この操作は2進数でも同じであり、「1」（10進数：1）という2進数を2倍（左にシフト）すると「10」（10進数：2）になり、1/2倍（右にシフト）すると「0.1」（10進数：0.5）です。

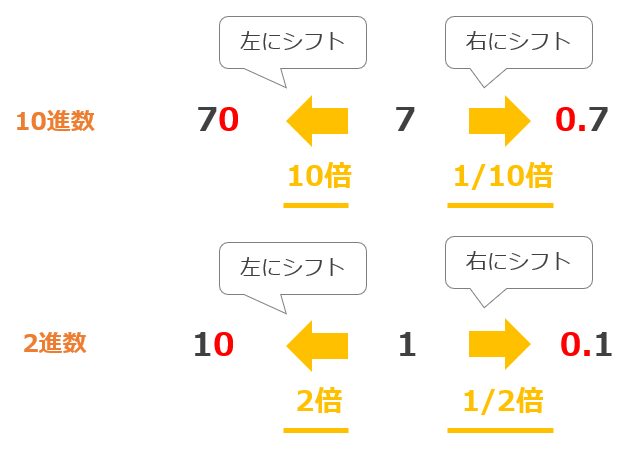
このように、ビット列を左にずらす（左にシフト）と元の値の2倍、右にずらす（右にシフト）と元の値の1/2倍という計算結果を簡単に得ることができます。コンピュータはこのシフト演算を使い、掛け算や割り算を行っています。

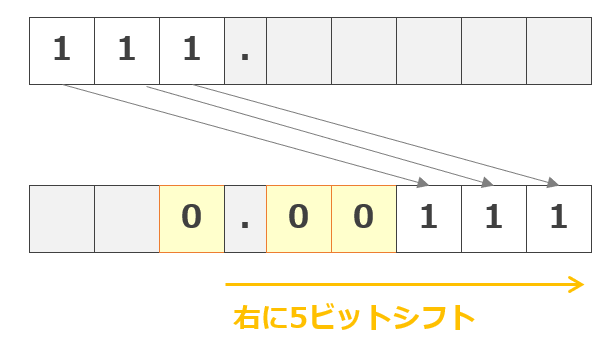
7÷32の「7」を2進数に変換すると「111」、さらに「32」を2の累乗で表現すると「2⁵」になります。今回は割り算なので「111」を「1/2⁵」倍すれば答えを求めることができます。

「1/2⁵」なので、次のように右に5ビットシフトすると「0.00111」となり、10進数の演算式「7÷32」の結果を2進数で求めることができました。

基本情報技術者試験おすすめの参考書・問題集

いちばんやさしい 基本情報技術者	『基本情報技術者試験』試験に、短期間で一発合格するための試験対策本。ITの知識がまったくない、未経験者やでもスラスラと学習を進められるよう、丁寧に解説。
かやのき先生の基本情報技術者教室	基本情報技術者をめざす方のためのやさしいオールインワンタイプの参考書＆問題集。イラストや豊富な図解・例え話を駆使して理解しやすく・記憶に残りやすいように説明。
基本情報技術者 パーフェクトラーニング過去問題集	科目A・Bともに万全の対策ができる、定番の過去問題集！科目A・科目Bの両方について万全の対策ができる。
キタミ式イラストIT塾 基本情報技術者	すべての解説をイラストベースで行っているため，とてもわかりやすい解説本。いちばん最初に読む基本情報技術者試験関連の書籍を探している人におすすめ！
出るとこだけ！基本情報技術者［科目B］	基本情報技術者【科目Ｂ】対策の定番書！前提知識＋解き方＋試験問題を掲載。効率よく学習できる。
基本情報技術者 合格教本	出題範囲を体系的にきちんと理解しながら学習したい人におすすめ！基本情報技術者試験の定番テキストの改訂版。
基本情報技術者 超効率の教科書＋よく出る問題集	動画でスムーズに学習スタート、テキストでしっかり理解度を深める！よく出る問題を反復学習することで、合格に直結するチカラが身に付く！