スケジュール管理でよく使われる図表である、ガントチャートそしてアローダイアグラム。
本記事では、アローダイアグラムについて分かりやすく解説していきます。
スポンサーリンク
目次
アローダイアグラムってなに?
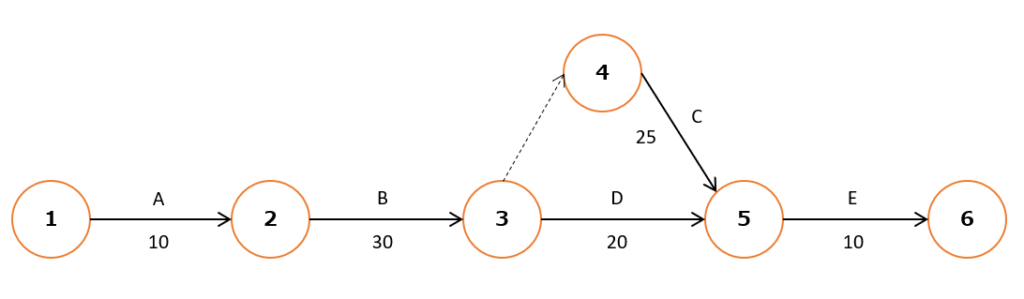
アローダイアグラムとは、作業の流れと、その作業に要する日数を分かりやすく図にあらわしたものです。



上記のアローダイアグラムは、以下の表をあらわしたモノです。
| 作業 | 作業日数 | 先行作業 | |
| A | システム設計 | 10日 | - |
| B | プログラミング | 30日 | A |
| C | データベース作成 | 25日 | B |
| D | システム試験 | 20日 | B |
| E | 受け入れ試験 | 10日 | C , D |
それでは、具体的にアローダイアグラムの作り方を解説していきます。
アローダイアグラムの作り方
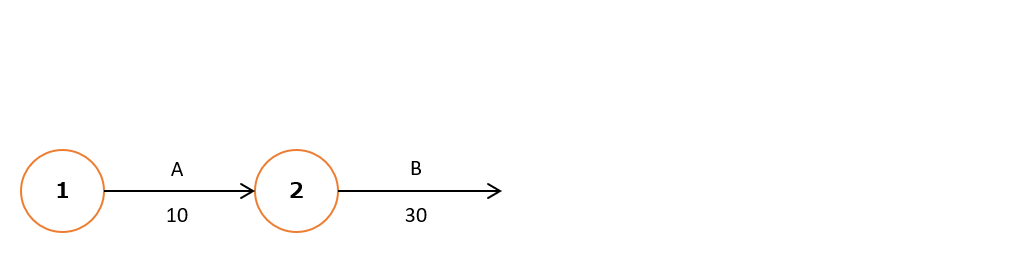
[手順1] 作業A「システム設計」をアローダイアグラムに追加
はじめの作業は、作業A「システム設計」です。
作業Aにかかる期間は10日間なので、①→は作業A、期間は10日とします。
[手順2] 作業B「プログラミング」をアローダイアグラムに追加
続いての作業は、作業B「プログラミング」です。
作業Bに着手するためには、作業Aが終わっていることが条件です。そのため作業Bは作業Aの後に書きます。
作業Bにかかる期間は30日間なので、②→は作業B、期間は30日とします。
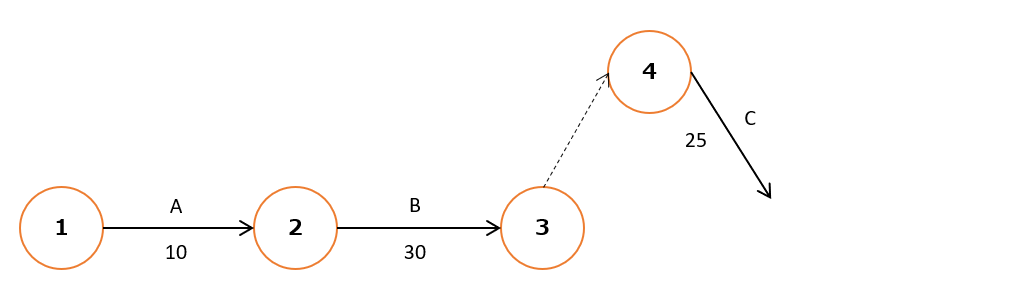
[手順3] 作業C「データベース作成」、作業D「システム試験」をアローダイアグラムに追加
続いての作業は、作業C「データベース作成」と作業D「システム試験」です。
作業C、作業Dに着手するためには、作業Bが終わっていることが条件です。そのため作業C、作業Dは作業Bの後に書きます。
まずは作業Cを追加します。アローダイアグラムは1つの結合点からは、一つの作業しか引けないので、ここでは点線(ダミー作業)を使用します。
作業Cにかかる期間は25日間なので、④→は作業C、期間は25日とします。
続いて作業Dを追加します。
作業Dにかかる期間は20日間なので、③→は作業D、期間は20日とします。
[手順4] 作業E「受け入れ試験」をアローダイアグラムに追加
最後に作業E「受け入れ試験」を追加します。
作業Eに着手するためには、作業Cと作業Dが終わっていることが条件です。そのため作業Eは作業Cと作業Dの後に書きます。
作業Eにかかる期間は10日間なので、⑤→は作業E、期間は10日とします。


アローダイアグラムで使用する記号
アローダイアグラムは、以下の3つの記号を使用して作成します。
| 記号 | 説明 |
 | 作業の開始と終了をあわらす記号で、結合点と呼びます。1つの結合点から開始できる作業は一つだけです。丸の中には先頭から順番に数値を割り当てます。 |
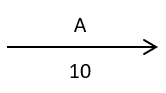 | 作業をあらわす矢印です。矢印の上には作業名、下には日数を記述します。 |
 | ダミー作業をあらわす矢印です。一つの結合点から開始できる作業は一つだけなので、複数の作業がある場合は、このダミー矢印を使用して開始位置となる結合点に導きます。 |
スポンサーリンク
アローダイアグラムでよく使われる用語
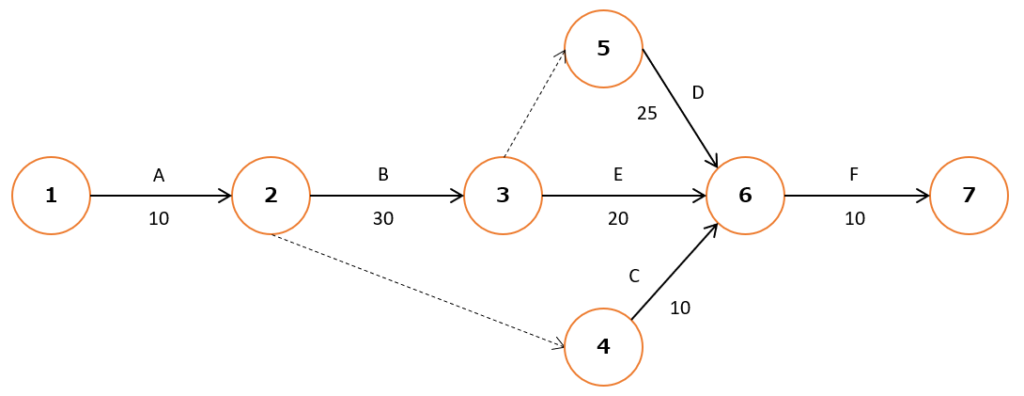
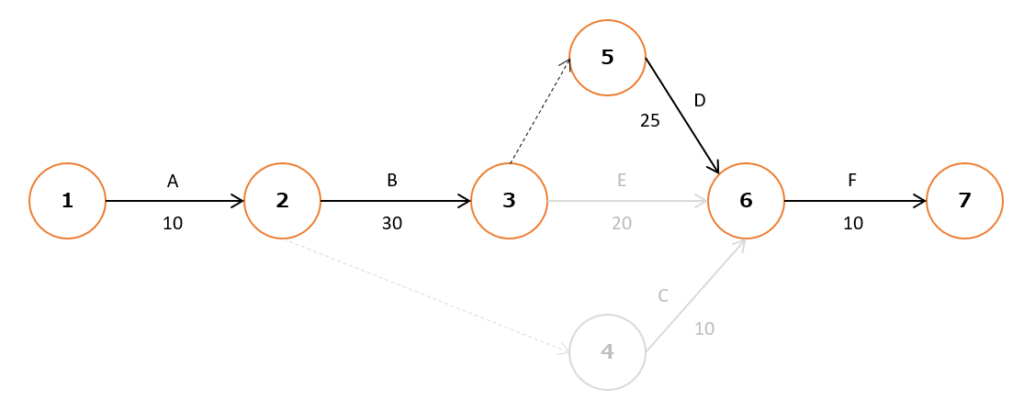
以下のアローダイアグラムを例に解説します。
| 作業 | 作業日数 | 先行作業 | |
| A | システム設計 | 10日 | - |
| B | プログラミング | 30日 | A |
| C | インフラ環境構築 | 10日 | A |
| D | データベース作成 | 25日 | B |
| E | システム試験 | 20日 | B |
| F | 受け入れ試験 | 10日 | C , D, E |
最早結合点時刻
最早結合点時刻とは、最も早く作業できる日時のことをいいます。
⑥の最早結合点時刻は、10日(A) + 30日(B) + 25日(D)で65日となります。(Fの作業を開始するにはC(10日)、D(25日)、E(20日)の作業が終わっていることが条件です。そのため一番日数のかかるDの25日を加算します)

最遅結合点時刻
最遅結合点時刻とは、全体に影響を与えない範囲で、作業の開始をどのくらい遅らせても平気かをあらわす日時のことをいいます。
④の作業は、本来ならAの作業(10日)が終わった日から作業を開始することができます。ただ⑥の最早結合点時刻は65日なので、65日 - Cの作業(10日)から作業を開始しても全体に影響を与えません。
したがって④の最遅結合点時刻は、65日 - 10日(C)で55日となります。

クリティカルパス
クリティカルパスとは、ルート上のどの作業が遅れても全体に影響が出るルートのことをいいます。そのため、クリティカルパス上のルートは日程的に余裕はなく、作業が遅れると問題です。
上図のように①→②→③→⑤→⑥→⑦がクリティカルパスであり、最長ルートと同じです。
クリティカルパス上にない作業Cと作業Eは、多少の作業遅れ(全体に影響がでない日数)があっても全体の日程には影響しません。しかしクリティカルパス上にある作業A、作業B、作業D、作業Fは作業の遅れが全体の日程に影響します。そのくらい重要なルートとなります。