目次
浮動小数点数
浮動小数点数とは、コンピュータにおける数値を表現する方法の一つで、主に小数点を含む数値を表現するときに利用されています。
浮動小数点数の形式
浮動小数点数は次のように「符号」「指数部」「仮数部」の形式で表現します。※32ビットの例

- 符号:正の数が0、負の数が1
- 指数部:2nのnの部分を2進数表記にした値を格納(負の数の場合は2の補数を使用)
- 仮数部:正規化した小数点以下の値を格納
浮動小数点数の「仮数部」には小数点以下の値が入り、指数部には2nのnを2進数にした値が入ります。

正規化とは
浮動小数点数の仮数部には正規化した値(小数点以下の値)が入ります。正規化とは、小数点の位置を調整し最上位桁を0以外の値にする作業のことです。
スポンサーリンク
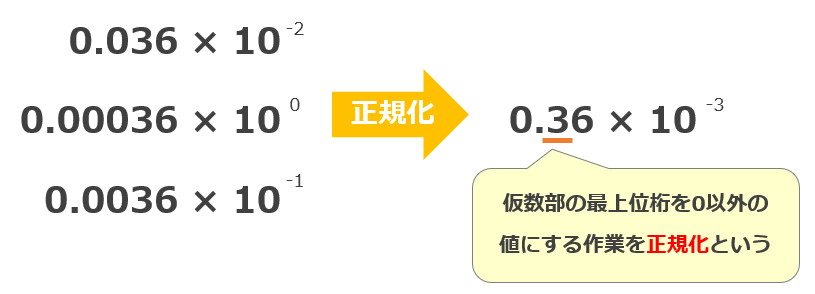
次の図は正規化のイメージ例です。
「0.036×10-2」「0.00036×100」「0.0036×10-1」は同じ値です。この値を「0.36×10-3」のように最上位桁を0以外の値にする作業のことを正規化といいます。
なぜ正規化が必要なのか?
浮動小数点数の仮数部は桁数が決まっています。そのため、有効桁数を超えた部分は丸め誤差により切り捨てられてしまいます。

例えば 0.036×102と0.36×101は同じ値です。ただし後者の方が仮数部の桁数は少なくすみます。(前者:036の3桁、後者:36の2桁)
正規化の目的は有効桁数を最大化し丸め誤差をできるだけ少なくすることです。仮数部の最上位桁を0以外に調整することで、丸め誤差が発生する頻度を減らすことができます。
浮動小数点数の設定手順
それでは、2進数の「0.01」を32ビットの浮動小数点数の形式で表現してみます。
仮数部の求め方
仮数部には2進数「0.01」を正規化した値が入ります。
0.01
↓ 正規化
0.1 × 2-1
仮数部には次のように正規化で求めた「0.1」の小数点以下の値が入ります。※足りない部分は0で埋める

指数部の求め方
指数部には2nのnを2進数に変換した値が入ります。今回は「0.1 × 2-1」なのでnは「-1」です。負の数の場合は次のように2の補数を使って2進数を求めます。
0000001 (10進数:1)
↓ すべてのビットを反転させる
1111110
↓ 1を加算する
1111111 (10進数:-1)
指数部には次のように「2-1」の「-1」を2進数に変えた値「1111111」が入ります。

符号の設定
最後に符号を設定すれば完成です。2進数「0.01」は正の数なので、符号には"0"を設定します。(0:正の数、1:負の数)

IEEE754の浮動小数点数
IEEE(米国電気電子学会)により規格化された、浮動小数点数形式のことを「IEEE754」といいます。
スポンサーリンク
IEEE754 浮動小数点数の形式
IEEE754の浮動小数点数は次の形式で表現します。※32ビットの例

IEEE754の特徴は「1.××」の形で正規化します。例えば、2進数「0.011」を正規化すると「0.11 × 2-1」になりますが、IEEE754の場合は、「1.1 × 2-2」となり1ビット多く保持することができます。(23ビットあれば24ビット分 表現できる)
- 符号:正の数が0、負の数が1
- 指数部:2nのnの部分に127(バイアス)を加算後、2進数表記にした値を格納
- 仮数部:1.××の形式で正規化した小数点以下の値を格納
IEEE754 浮動小数点数の設定手順
それでは、2進数の「0.01」を32ビットのIEEE754形式の浮動小数点数で表現してみます。
仮数部の求め方(IEEE754)
仮数部には2進数「0.011」を1.××形式に正規化した値が入ります。
0.011
↓ 正規化
1.1 × 2-2
仮数部には次のように正規化で求めた「1.1」の小数点以下の値が入ります。※足りない部分は0で埋める

指数部の求め方(IEEE754)
指数部には2nのnにバイアスと呼ばれる127を加算した結果を2進数に変換した値が入ります。
バイアスには「ゲタをはかせる」(ゲタ履き表現)という意味があり、指数部にバイアスを加算することで、負の数を含む表現が正の数だけで表現できます。
今回の例では「1.1 × 2-2」とnの部分が「-2」なので「-2」にバイアスの「127」を加算します。
-2 + 127 = 125
↓ 2進数に変換
01111101
バイアス値を加算した結果である「125」を2進数に変えた値「01111101」が指数部に入ります。

符号の設定(IEEE754)
2進数「0.01」は正の数なので符号には"0"を設定します。(0:正の数、1:負の数)

浮動小数点数の誤差
浮動小数点数では、表現できる数の範囲が決まっています。(32ビット形式の浮動小数点数では、仮数部で表現できるビットは24ビット※IEEE754は23ビット)
例えば、2進数「0.00011001100110011001100110011...」(10進数の0.1) のように割り切れなくて無限に続く小数などは「決められた範囲」に収まりません。
そこで、コンピュータはこれらの数をあらわす時「なるべく近い値」を使用します。その結果、実際の値と誤差が生じてしまいます。
コンピュータで発生する誤差には次のような種類があります。
| 誤差の種類 | 説明 |
| 丸め誤差 | 「表現できる数の範囲」(有効桁)を超えてしまった際に有効桁以降を切り捨てることによって発生する誤差。 |
| 打切り誤差 | コンピュータの計算処理を途中で打ち切ることにより発生する誤差。 |
| 桁落ち | 値がほぼ等しい数値の差を求めた時に発生する誤差。 |
| 情報落ち | 大きい値と小さい値の数値を和もしくは差を求めた時に発生する誤差。 |

