問題
クイックソートの処理方法を説明したものはどれか。
- ア:既に整列済みのデータ列の正しい位置に,データを追加する操作を繰り返していく方法である。
- イ:データ中の最小値を求め,次にそれを除いた部分の中から最小値を求める。この操作を繰り返していく方法である。
- ウ:適当な基準値を選び,それより小さな値のグループと大きな値のグループにデータを分割する。同様にして,グループの中で基準値を選び,それぞれのグループを分割する。この操作を繰り返していく方法である。
- エ:隣り合ったデータの比較と入替えを繰り返すことによって,小さな値のデータを次第に端のほうに移していく方法である。
基本情報技術者平成30年秋期 午前問6
基本情報技術者試験や応用情報技術者試験で出題される整列アルゴリズムの問題。各整列アルゴリズムの動きを理解していれば、そこまで難しい問題ではありませんが、理解してないと問題を解くのは困難です。
整列アルゴリズムには基本的な整列アルゴリズム(基本交換法、基本選択法、基本挿入法)と高速な整列アルゴリズム(シェルソート、クイックソート、マージソート、ヒープソート)があります。
本記事では、整列アルゴリズムについて図解で分かりやすく解説しています。
本記事で学べること
- 基本的な整列アルゴリズム(基本交換法、基本選択法、基本挿入法)の動きを理解する
- 高速な整列アルゴリズム(シェルソート、クイックソート、マージソート、ヒープソート)の動きを理解する
- 基本情報技術者試験の過去問の解き方を学ぶ
目次
基本的な整列アルゴリズム
基本的な整列アルゴリズムには次の手法があります。
| 基本的な整列アルゴリズム | 説明 |
| 基本交換法(バブルソート) | 隣り合わせのデータ同士を比較して交換を繰り返していく手法 |
| 基本選択法(選択ソート) | 未整列の配列の中から最小値(もしくは最大値)を探し先頭のデータと交換する作業を繰り返していく手法 |
| 基本挿入法(挿入ソート) | 未整列の配列から1つずつ値を取り出し整列済み配列の適切な位置へ挿入していく手法 |
スポンサーリンク
基本交換法(バブルソート)
基本交換法(バブルソート)とは、隣り合わせのデータ同士を比較して交換を繰り返していく手法です。

例題
未整列の配列「4, 1, 3, 2」を基本交換法で整列させよ。
1巡目 先頭から順番に隣り合わせの値と比較していく
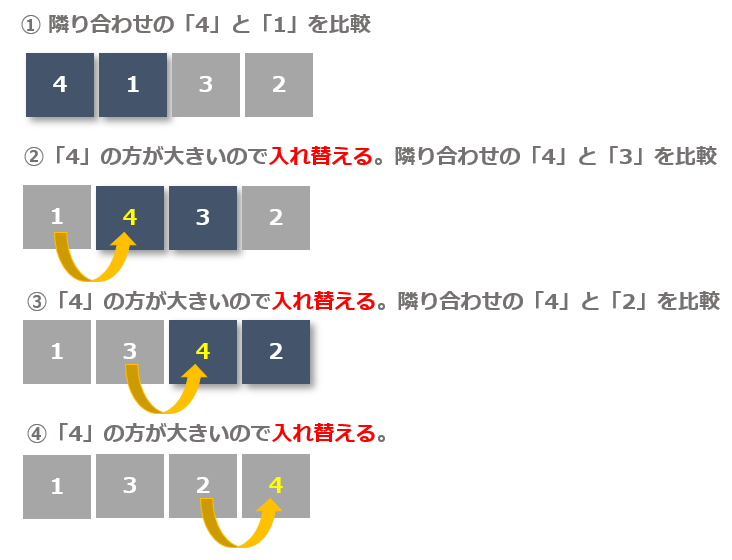
まずは先頭から順に隣り合わせの値と比較していきます。
1巡目の流れ
- 先頭の「4」と隣の「1」を比較、「4」の方が大きいので入れ替える
- 2番目の「4」と隣の「3」を比較、「4」の方が大きいので入れ替える
- 3番目の「4」と隣の「2」を比較、「4」の方が大きいので入れ替える
2巡目 再び先頭から順番に隣り合わせの値と比較していく
1巡目は入れ替えが発生したので、再び先頭から順番に隣り合わせの値と比較していきます。
2巡目の流れ
- 先頭の「1」と隣の「3」を比較、「1」の方が小さいのでそのまま
- 2番目の「3」と隣の「2」を比較、「3」の方が大きいので入れ替える
- 3番目の「3」と隣の「4」を比較、「3」の方が小さいのでそのまま
3巡目 再び先頭から順番に隣り合わせの値と比較していく
2巡目は入れ替えが発生したので、再び先頭から順番に隣り合わせの値と比較していきます。
2巡目の流れ
- 先頭の「1」と隣の「2」を比較、「1」の方が小さいのでそのまま
- 2番目の「2」と隣の「3」を比較、「2」の方が小さいのでそのまま
- 3番目の「3」と隣の「4」を比較、「3」の方が小さいのでそのまま

基本選択法(選択ソート)
基本選択法(選択ソート)とは、未整列の配列の中から最小値(もしくは最大値)を探し先頭のデータと交換する作業を繰り返していく手法です。

例題
未整列の配列「4, 1, 3, 2」を基本選択法で整列させよ。
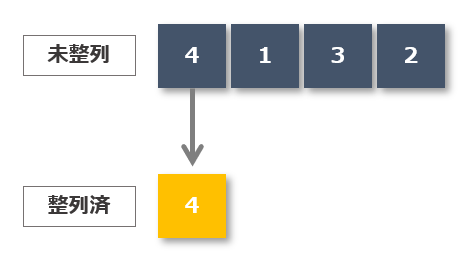
1回目 未整列データの中から最小値を探し先頭の値と入れ替える
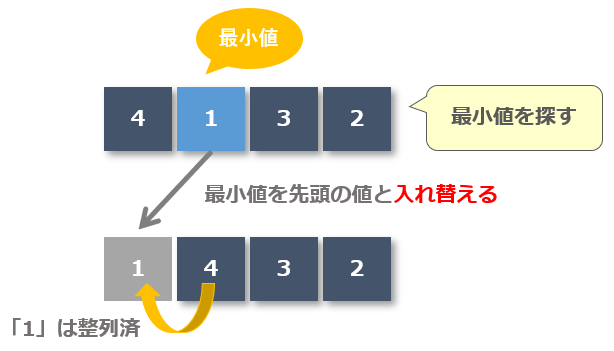
未整列データの中から最小値を探し先頭の値と入れ替え、入れ替えた値を整列済みとします。(最小値「1」と先頭「4」を入れ替え、「1」を整列済みにする)
1回目の流れ
- 未整列データの中から最小値を探す
- 最小値「1」と先頭の値「4」を入れ替える
- 最小値「1」を整列済みにする
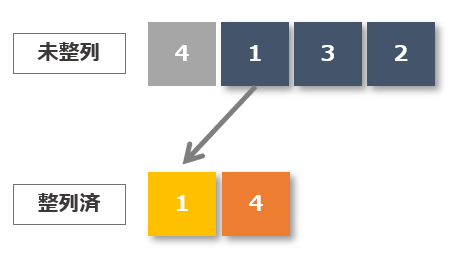
2回目 再び未整列データの中から最小値を探し先頭の値と入れ替える
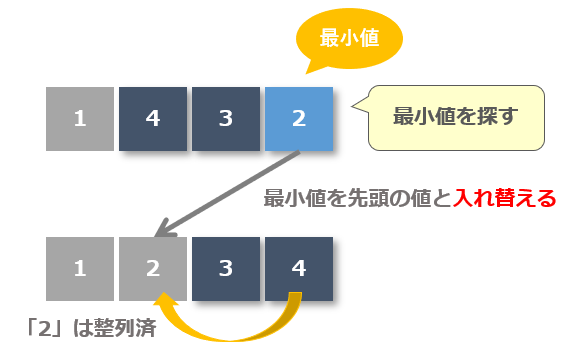
整列済みデータ以外の未整列データの中から最小値を探し先頭の値と入れ替え、入れ替えた値を整列済みとします。(最小値「2」と先頭「4」を入れ替え、「2」を整列済みにする)
2回目の流れ
- 整列済みを除く未整列データの中から最小値を探す
- 最小値「2」と先頭の値「4」を入れ替える
- 最小値「2」を整列済みにする
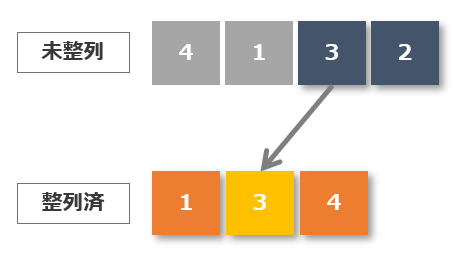
3回目 再び未整列データの中から最小値を探す
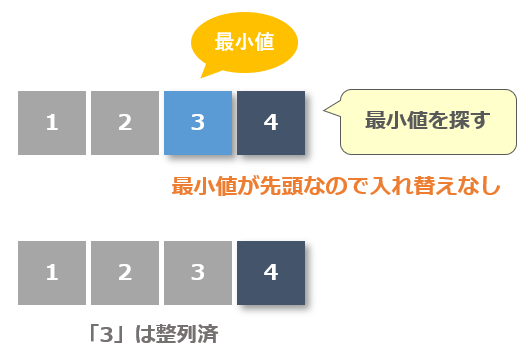
整列済みデータ以外の未整列データの中から最小値を探します。最小値「3」は先頭の値なので入れ替えはおこなわずそのままとします。
3回目の流れ
- 整列済みを除く未整列データの中から最小値を探す
- 最小値「3」は先頭の値なので入れ替えはおこなわずそのままとする
- 最小値「3」を整列済みにする
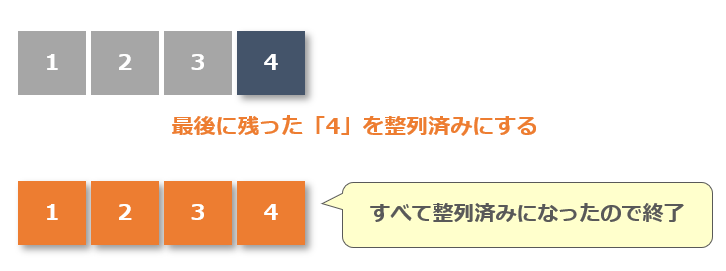
4回目 最後の値を整列済みにして完了
最後に残った値「4」を整列済みにします。

スポンサーリンク
基本挿入法(挿入ソート)
基本挿入法(挿入ソート)とは、未整列の配列から1つずつ値を取り出し整列済み配列の適切な位置へ挿入していく手法です。

例題
未整列の配列「4, 1, 3, 2」を基本挿入法で整列させよ。
未整列1番目を整列済みに挿入
未整列データの1番目「4」を整列済みデータに挿入します。
未整列2番目を整列済みに挿入
未整列データの2番目「1」を整列済みデータに挿入します。整列済みデータの1番目「4」と「1」を比較し「1」の方が小さいので「4」の前に挿入します。
未整列3番目を整列済みに挿入
未整列データの3番目「3」を整列済みデータに挿入します。整列済みデータの末尾の値から順番に比較、「3」は「1」より大きく「4」より小さいので「1」と「4」の間に挿入します。
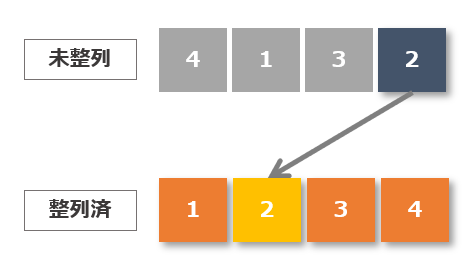
未整列4番目を整列済みに挿入
未整列データの4番目「2」を整列済みデータに挿入します。整列済みデータの末尾の値から順番に比較、「2」は「1」より大きく「3」より小さいので「1」と「3」の間に挿入します。

高速な整列アルゴリズム
高速な整列アルゴリズムには次の手法があります。
| 高速な整列アルゴリズム | 説明 |
| シェルソート | ある一定間隔おきに取り出した要素内で並び替えを繰り返していく手法 |
| クイックソート | 適当な基準値を選び、それより小さな値のグループと大きな値のグループに分ける作業を繰り返して整列していく手法 |
| マージソート | 要素数が1になるまで2分割を繰り返し、整列しながら戻していく手法 |
| ヒープソート | 木構造を利用して並び替えを行う手法 |
シェルソート
シェルソートとは、ある一定間隔おきに取り出した要素内で並び替えを繰り返していく手法です。
基本的な整列アルゴリズムである基本挿入法(挿入ソート)は、ある程度整列されたデータに対しては高速だが、あまり整列されていないデータに対しては低速です。
シェルソートは一定間隔でグループ分けして並び替えを繰り返していくことで、ある程度整列されたデータを作ることができ、基本挿入法(挿入ソート)の長所を生かした手法です。

例題
未整列の配列「4, 3, 5, 7, 1, 8, 6, 2」をシェルソートで整列させよ。
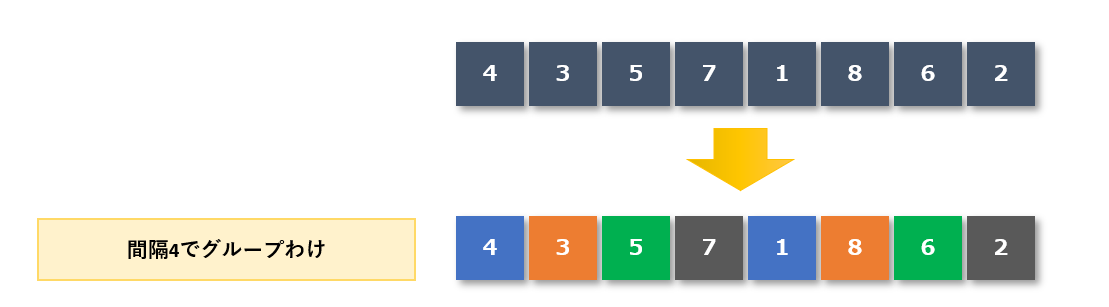
一定間隔おきにグループ分けをおこなう(間隔4)
まずは一定間隔おきにグループ分けをおこないます。次の例では間隔4でグループ分けします。
- 青色グループ:4,1
- 橙色グループ:3,8
- 緑色グループ:5,6
- 黒色グループ:7,2
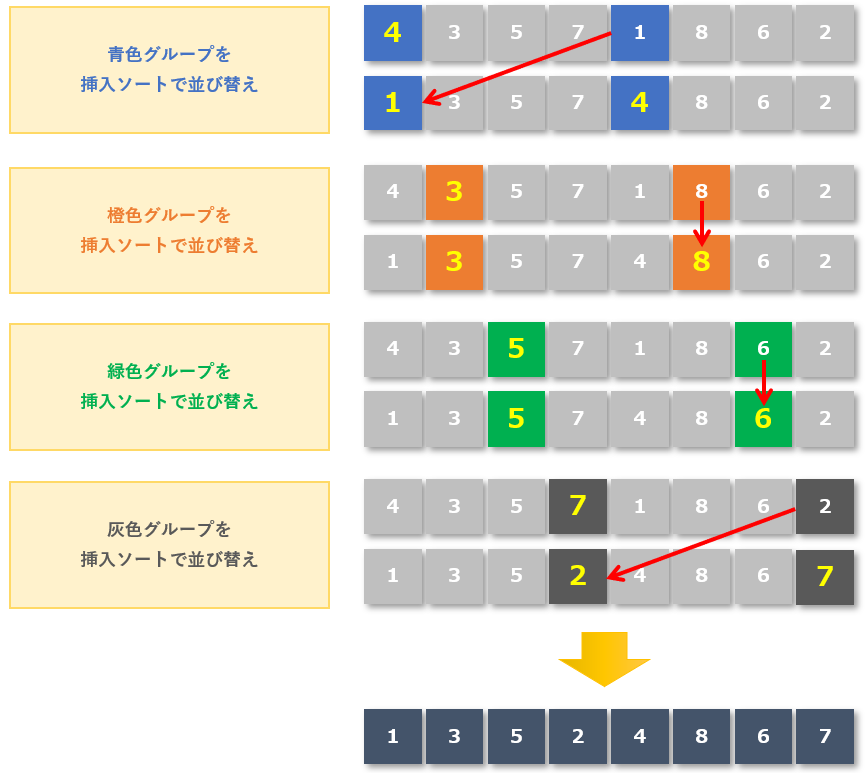
同じグループ内で並び替えをおこなう(間隔4)
基本挿入法(挿入ソート)を使い同じグループ内で並び替えをおこないます。
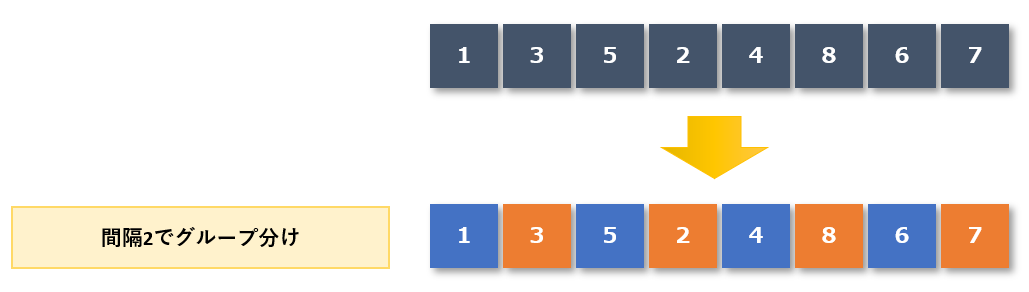
一定間隔を縮めて再びグループ分けをおこなう(間隔2)
一定間隔を4から2に縮めて再びグループ分けをおこないます。
- 青色グループ:1,5,4,6
- 橙色グループ:3,2,8,7
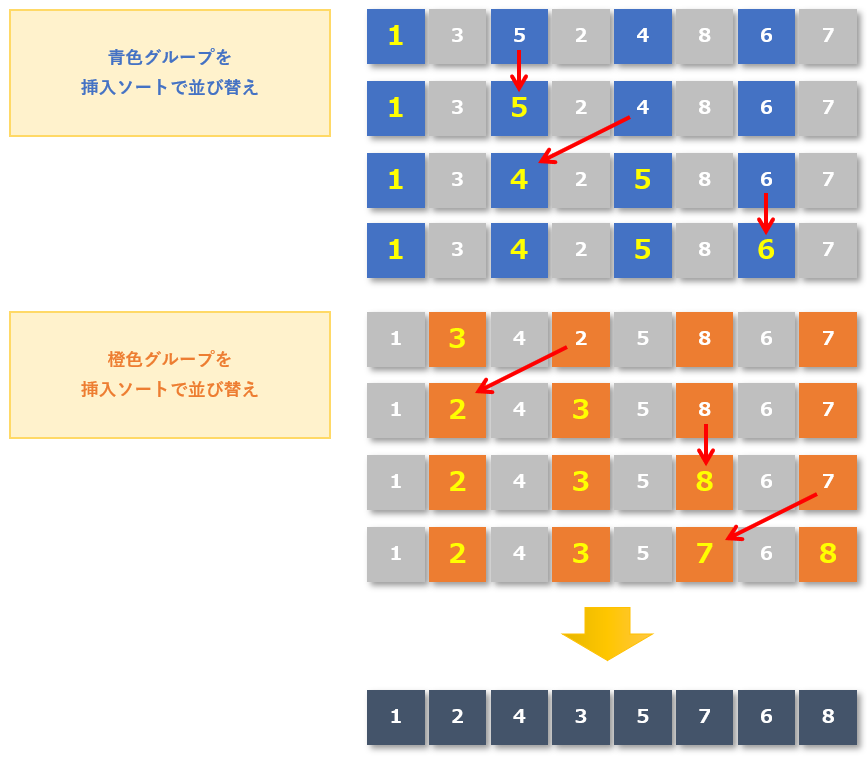
同じグループ内で並び替えをおこなう(間隔2)
基本挿入法(挿入ソート)を使い同じグループ内で並び替えをおこないます。
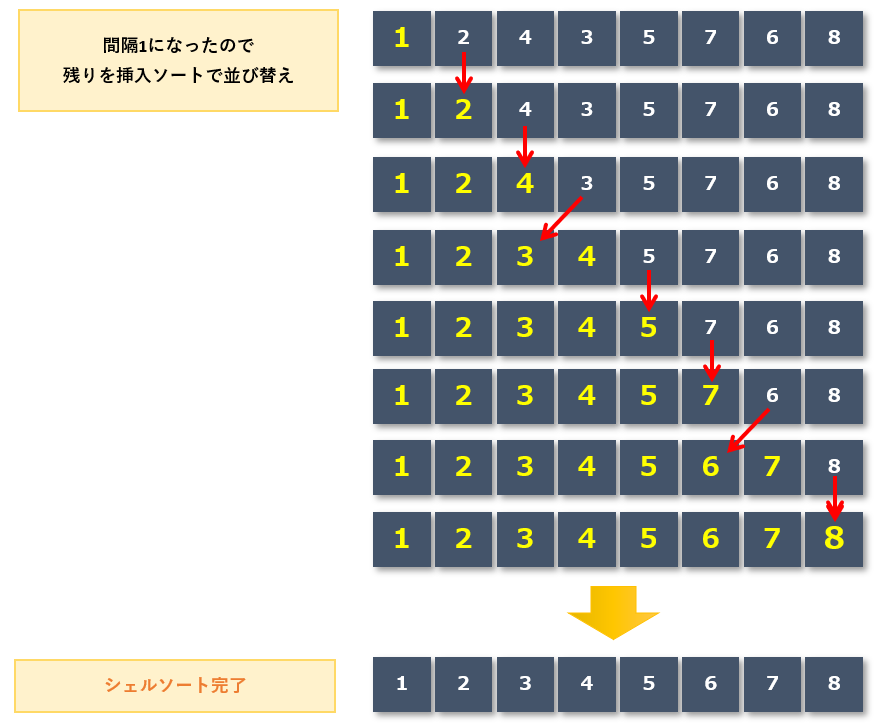
間隔1になったら残りの要素を並び替える
一定間隔が1になったのでグループ分けは行わず、残りのデータを挿入ソートで並び替えをしていきます。

スポンサーリンク
クイックソート
クイックソートとは、適当な基準値を選び、それより小さな値のグループと大きな値のグループに分ける作業を繰り返して整列していく手法です。

例題
未整列の配列「4, 3, 5, 7, 1, 8, 6, 2」をクイックソートで整列させよ。
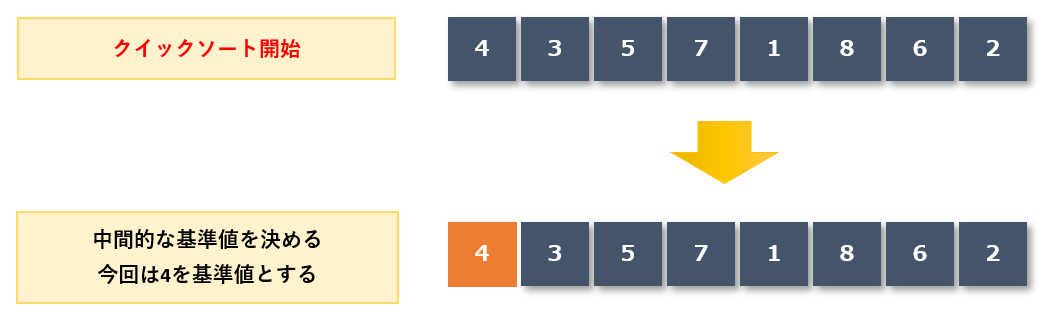
基準値を定める
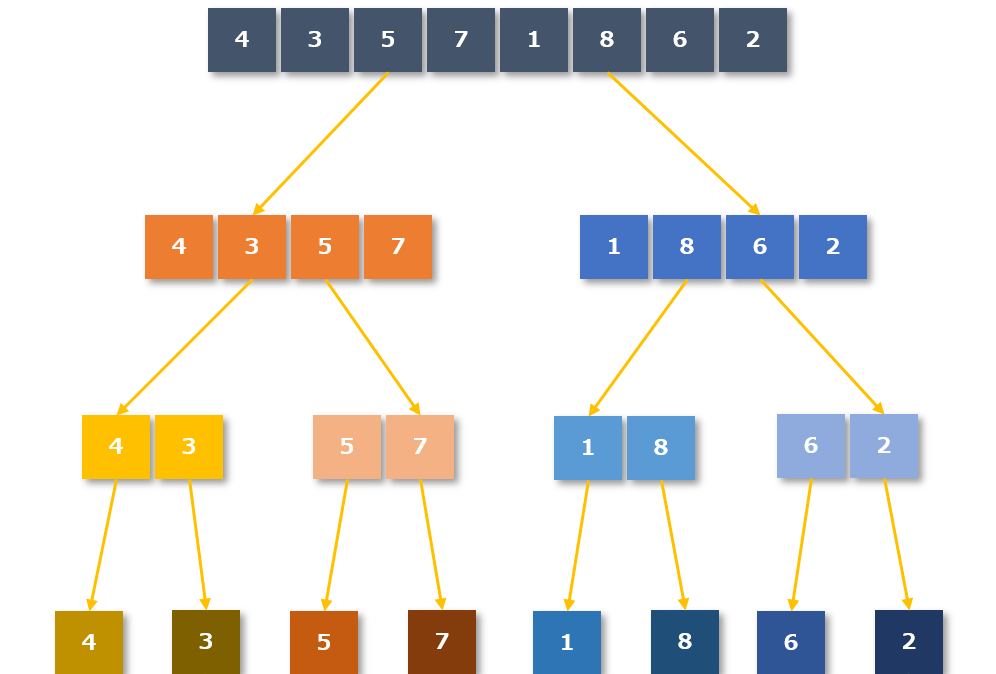
まずは適当な基準値を決めます。今回の例では中央付近の値である「4」を基準値とします。
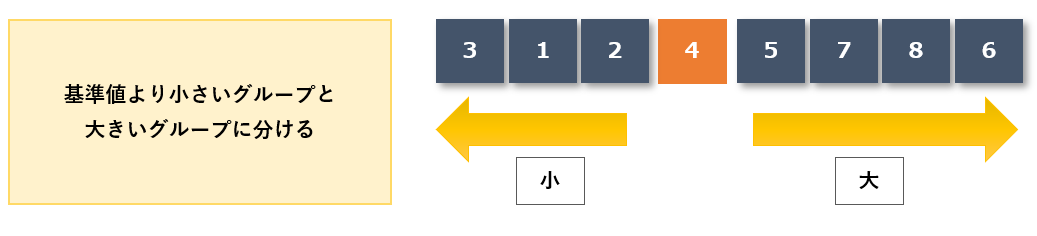
基準値より小さな値のグループと大きな値のグループに分ける
基準値「4」より小さい値のグループと大きい値のグループに分けます。
- 小さい値のグループ:3,1,2
- 大きい値のグループ:5,7,8,6
基準値「4」の位置は確定
小さい値のグループ内で基準値を定め、基準値より小さな値のグループと大きな値のグループに分ける
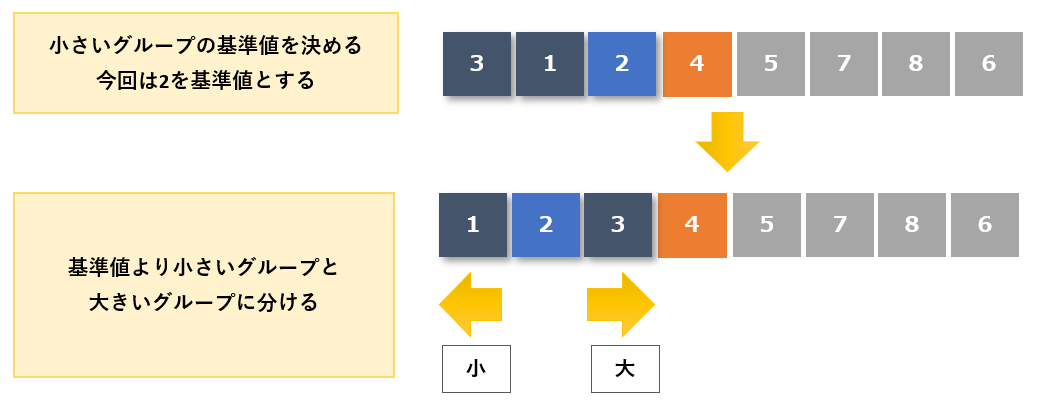
小さい値のグループから適当な基準値を決めます。今回の例では中央値である「2」を基準値とし、基準値「2」より小さい値のグループと大きい値のグループに分けます。
- 小さい値のグループ:1
- 大きい値のグループ:3
小さい値と大きい値のグループには値が1つしかないので「1」「3」と基準値「2」の位置は確定
大きい値のグループ内で基準値を定め、基準値より小さな値のグループと大きな値のグループに分ける
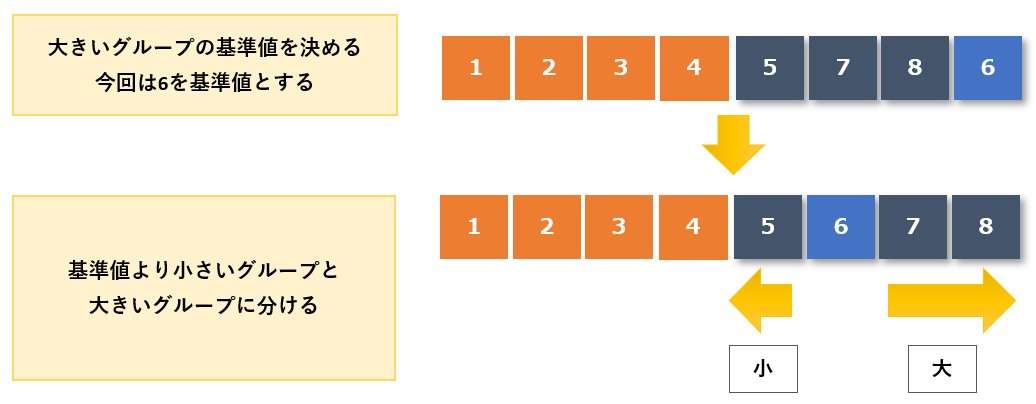
大きい値のグループから適当な基準値を決めます。今回の例では中央付近の値である「6」を基準値とし、基準値「6」より小さい値のグループと大きい値のグループに分けます。
- 小さい値のグループ:5
- 大きい値のグループ:7,8
小さい値のグループには値が1つしかないので「5」と基準値「6」の位置は確定
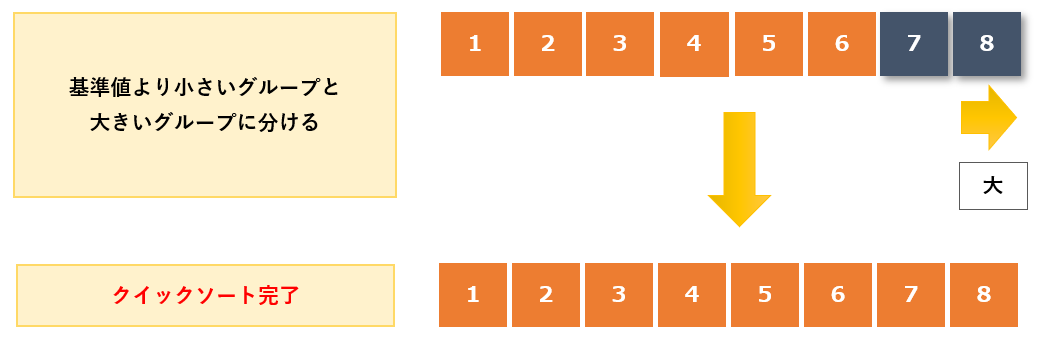
最後に7もしくは8を基準値(今回の例では7を基準値とする)として、7,8の並び順を確定させれば終了です。(7,8はすでに整列されているのでそのまま)
- 大きい値のグループ:8
大きい値のグループには値が1つしかないので「8」と基準値「7」の位置は確定

マージソート
マージソートとは、要素数が1になるまで2分割を繰り返し、整列しながら戻していく手法です。

例題
未整列の配列「4, 3, 5, 7, 1, 8, 6, 2」をマージソートで整列させよ。
要素数が1になるまで2分割を繰り返す
まずは要素数が1になるまで2分割を繰り返していきます。
- 未整列のデータ「4, 3, 6, 7, 1, 8, 6, 2」を2分割する
- 2分割:「4, 3, 5, 7」「1, 8, 6, 2」
- 更に2分割:「4, 3」「5, 7」「1, 8」「6, 2」
- 更に2分割:「4」「3」「5」「7」「1」「8」「6」「2」
※要素数が1になったので2分割はここで終了
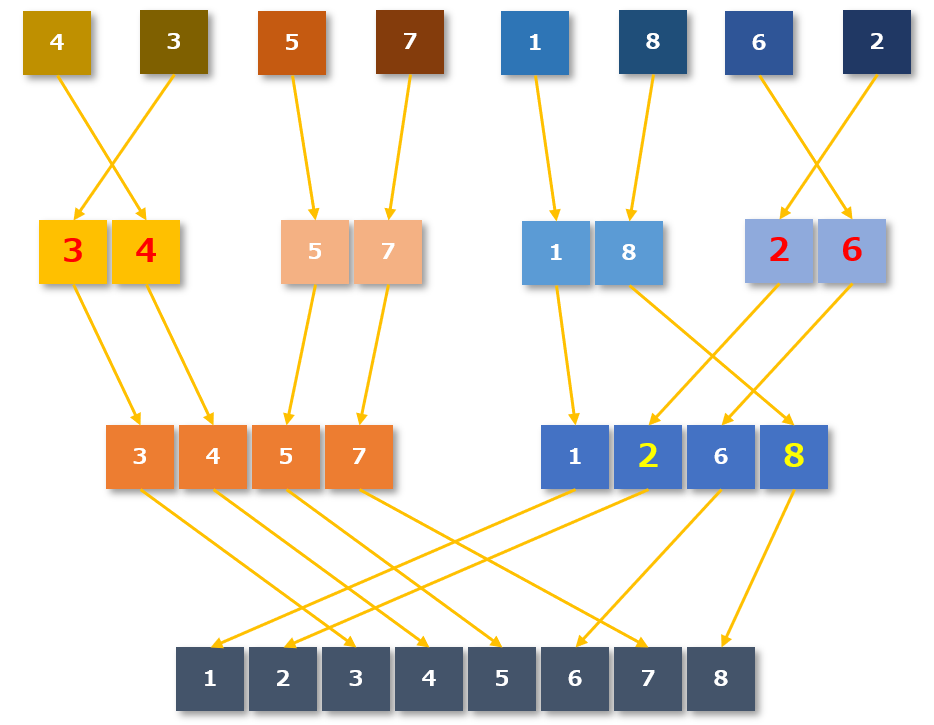
2分割した要素を並び替えしながら戻していく
次に2分割した要素を並び替えしながら戻していきます。
- 分割された要素:「4」「3」「5」「7」「1」「8」「6」「2」
- 並び替えしながら戻す:「3, 4」「5, 7」「1, 8」「2, 6」
- 並び替えしながら戻す:「3, 4, 5, 7」「1, 2, 6, 8」
- 並び変えしながら戻す:「1, 2, 3, 4, 5, 6, 7, 8」

ヒープソート
ヒープソートとは、「順序木」といわれる木構造の構成にして、そこから最大値または最小値を取り出して整列、これを繰り返すことで全体を整列させる手法です。
ヒープソートの解説はこちら
基本情報技術者試験 過去問の解説
スポンサーリンク
基本情報技術者平成30年秋期 午前問6
問題
クイックソートの処理方法を説明したものはどれか。
- ア:既に整列済みのデータ列の正しい位置に,データを追加する操作を繰り返していく方法である。
- イ:データ中の最小値を求め,次にそれを除いた部分の中から最小値を求める。この操作を繰り返していく方法である。
- ウ:適当な基準値を選び,それより小さな値のグループと大きな値のグループにデータを分割する。同様にして,グループの中で基準値を選び,それぞれのグループを分割する。この操作を繰り返していく方法である。
- エ:隣り合ったデータの比較と入替えを繰り返すことによって,小さな値のデータを次第に端のほうに移していく方法である。
基本情報技術者平成30年秋期 午前問6
クイックソートとは、適当な基準値を選び、それより小さな値のグループと大きな値のグループに分ける作業を繰り返して整列していく手法です。
クイックソートの説明として正しいのはどれか、解答のア~エを順番に確認していきます。
解答ア
ア:既に整列済みのデータ列の正しい位置に,データを追加する操作を繰り返していく方法である。
→ 基本挿入法(挿入ソート)の説明なので不正解
解答イ
イ:データ中の最小値を求め,次にそれを除いた部分の中から最小値を求める。この操作を繰り返していく方法である。
→ 基本選択法(選択ソート)の説明なので不正解
解答ウ
ウ:適当な基準値を選び,それより小さな値のグループと大きな値のグループにデータを分割する。同様にして,グループの中で基準値を選び,それぞれのグループを分割する。この操作を繰り返していく方法である。
→ クイックソートの説明なので正解
解答エ
エ:隣り合ったデータの比較と入替えを繰り返すことによって,小さな値のデータを次第に端のほうに移していく方法である。
→ 基本交換法(バブルソート)の説明なので不正解