問題
問題
2分探索に関する記述のうち,適切なものはどれか。
- ア:2分探索するデータ列は整列されている必要がある。
- イ:2分探索は線形探索より常に速く探索できる。
- ウ:2分探索は探索をデータ列の先頭から開始する。
- エ:n個のデータの探索に要する比較回数は,nlog2nに比例する。
基本情報技術者平成26年秋期 午前問6
基本情報技術者試験や応用情報技術者試験で出題される探索アルゴリズムの問題、探索アルゴリズムには「線形探索」「2分探索」「ハッシュ法」などがあり、過去問では「線形探索」「2分探索」「ハッシュ法」がどのような動きをするか問われる問題が出題されています。
本記事では、探索アルゴリズムについて図解で分かりやすく解説しています。
本記事で学べること
- 探索アルゴリズムについて理解する
- 線形探索、2分探索、ハッシュ法の動きを理解する
- 基本情報技術者試験の過去問の解き方を学ぶ
目次
探索アルゴリズム
探索アルゴリズムとは、配列のような複数のデータが格納されている箱の中から目的のデータを探しだすアルゴリズムのことです。
基本情報技術者試験で主に出題される探索アルゴリズムには「線形探索」「2分探索」「ハッシュ法」があります。
スポンサーリンク
線形探索(せんけいたんさく)
線形探索は非常にシンプルな探索アルゴリズムであり、目的のデータを先頭から順に探索していく手法です
先頭から順に探索していき、目的のデータが見つかる もしくは 配列のデータをすべて確認したら線形探索は終了です。

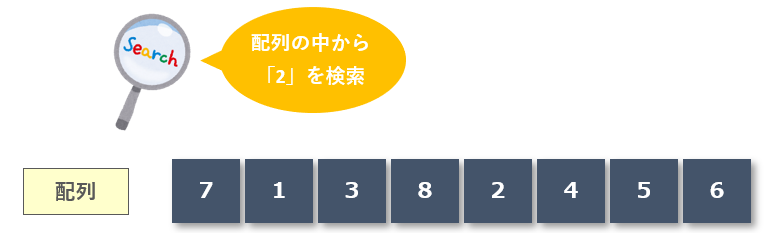
線形探索の流れ
線形探索は目的のデータを先頭から順に探索していく手法です。そのため先頭の要素から順番に確認してきます。
先頭の要素は「7」なので「7」と「2」を比較します。目的のデータではないので次へ

続いて次の要素「1」と「2」を比較します。目的のデータではないので次へ

続いて次の要素「3」と「2」を比較します。目的のデータではないので次へ

続いて次の要素「8」と「2」を比較します。目的のデータではないので次へ

続いて次の要素「2」と「2」を比較します。目的のデータがあったので線形探索を終了します。

暗記メモ
- 線形探索は先頭から順に目的のデータを探索するアルゴリズム
2分探索(にぶんたんさく)
2分探索は「昇順」または「降順」に並んでいる配列やリストに対して探索を行う手法です。
探索対象を1/2ずつ削り落としていくので効率よく探索することができます。

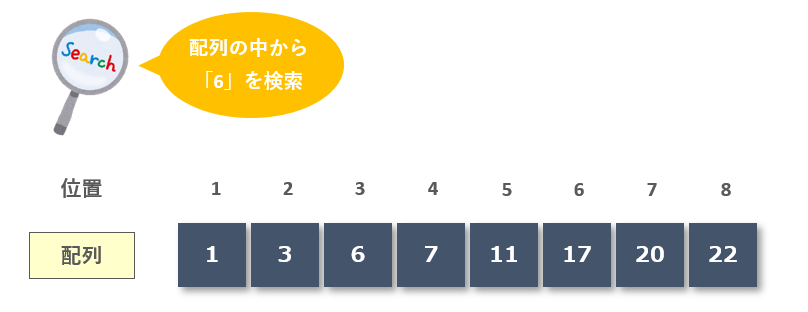
2分探索の流れ
2分探索は探索対象を1/2ずつ削り落としていく手法です。整列された配列の中央位置のデータと目的のデータを比較して、探索範囲を半分に絞り込んでいきます。
まずは配列の中央位置を計算します。(最小位置:1、最大位置:8)
中央位置の計算方法は次のとおり。
最小位置 + (最大位置 - 最小位置) / 2
今回の例の最小位置は「1」、最大位置は「8」なので「1 + (8 - 1) / 2 = 4」と中央位置を求めます。
計算した結果、配列の中央位置は「4」なので、位置4のデータ「7」と「6」比較します。比較した結果「6」の方が小さいので、探索の範囲を左半分に絞り込みます。

続いては位置1~3の中央位置を計算します。(最小位置:1、最大位置:3)
今回の例の最小位置は「1」、最大位置は「3」なので「1 + (3 - 1) / 2 = 2」と中央位置を求めます。
計算した結果、配列の中央位置は「2」なので、位置2のデータ「3」と「6」を比較します。比較した結果「6」の方が大きいので、探索の範囲を右半分に絞り込みます。
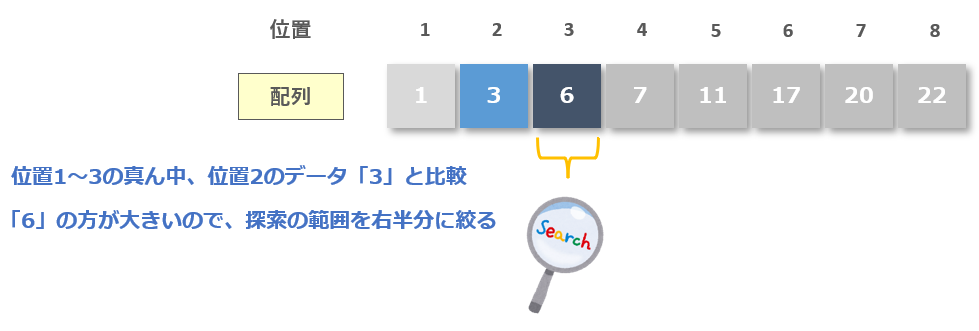
最後に「6」と比較、「6」を見つけることができたので探索終了です。

暗記メモ
- 2分探索は探索範囲を1/2に狭めることを繰り返して目的のデータを探索するアルゴリズム

- 平均比較回数:(log2n)回
- 最大比較回数:(log2n)+1回
スポンサーリンク
ハッシュ法
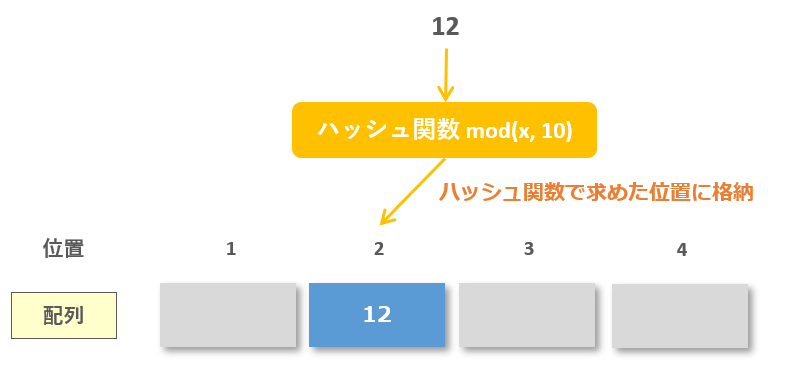
ハッシュ法とは、一定の計算式(ハッシュ関数)を用いてデータの格納位置(格納アドレス)を特定する手法です。
例えば、一定の計算式を「mod(x, 10) 」とし「12」を配列に格納すると、次のように位置「2」の場所に格納されます。
※modは余りが返ってくる関数であり、mod(x, 10)は、xを10で割ったときの余りが返ってくる
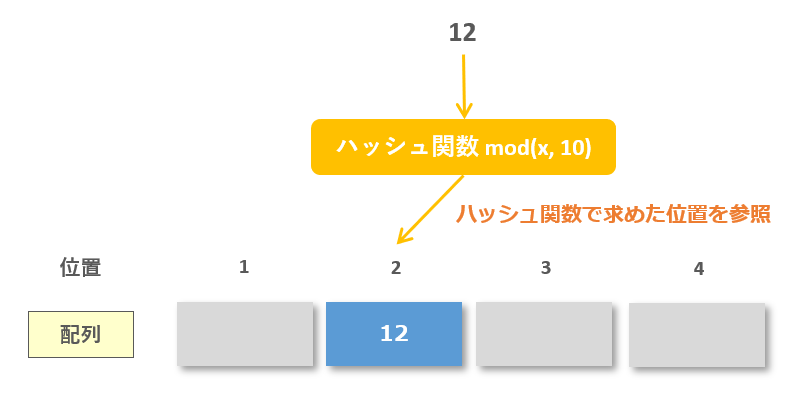
ハッシュ法を使って目的のデータを探索するときも格納したときと同じ計算式「mod(x, 10)」を使い、格納位置を特定します。
暗記メモ
- ハッシュ法は一定の計算式を用いてデータの格納位置を特定する手法
- 線形探索法や2分探索法とは異なり、常に一定の時間(探索回数1回)で目的のデータを探索することができる
基本情報技術者試験 過去問の解説
基本情報技術者令和元年秋期 午前問10
問題
この問題は、設問のとおりハッシュ関数 mod(a1+a2+a3+a4+a5,13) に54321をあてはめて計算し、配列のどの位置に入るか求めます。
mod(5+4+3+2+1,13) = mod(15, 13) = 2
※15÷13の余りは2

基本情報技術者平成26年秋期 午前問6
問題
2分探索に関する記述のうち,適切なものはどれか。
- ア:2分探索するデータ列は整列されている必要がある。
- イ:2分探索は線形探索より常に速く探索できる。
- ウ:2分探索は探索をデータ列の先頭から開始する。
- エ:n個のデータの探索に要する比較回数は,nlog2nに比例する。
基本情報技術者平成26年秋期 午前問6
2分探索とは「昇順」または「降順」に並んでいる配列に対して探索範囲を半分に狭めることを繰り返して目的のデータを探索するアルゴリズムです。
解答ア
ア:2分探索するデータ列は整列されている必要がある。
→ 2分探索を行うにはデータが整列されていることが条件なので正解です。
解答イ
イ:2分探索は線形探索より常に速く探索できる。
→ 2分探索は線形探索よりも効率よく目的のデータを見つけることができるが、目的のデータが先頭にある場合は線形探索の方が早く処理ができるため不正解です。
解答ウ
ウ:2分探索は探索をデータ列の先頭から開始する。
→ 探索をデータ列の先頭から開始するのは、線形探索なので不正解です。
解答エ
エ:n個のデータの探索に要する比較回数は,nlog2nに比例する。
→ 2分探索の平均比較回数を求める式は log2n なので不正解です。

基本情報技術者試験おすすめの参考書・問題集
| いちばんやさしい 基本情報技術者 | 『基本情報技術者試験』試験に、短期間で一発合格するための試験対策本。ITの知識がまったくない、未経験者やでもスラスラと学習を進められるよう、丁寧に解説。 |
| かやのき先生の基本情報技術者教室 | 基本情報技術者をめざす方のためのやさしいオールインワンタイプの参考書&問題集。イラストや豊富な図解・例え話を駆使して理解しやすく・記憶に残りやすいように説明。 |
| 基本情報技術者 パーフェクトラーニング過去問題集 | 科目A・Bともに万全の対策ができる、定番の過去問題集!科目A・科目Bの両方について万全の対策ができる。 |
| キタミ式イラストIT塾 基本情報技術者 | すべての解説をイラストベースで行っているため,とてもわかりやすい解説本。いちばん最初に読む基本情報技術者試験関連の書籍を探している人におすすめ! |
| 出るとこだけ!基本情報技術者[科目B] | 基本情報技術者【科目B】対策の定番書!前提知識+解き方+試験問題を掲載。効率よく学習できる。 |
| 基本情報技術者 合格教本 | 出題範囲を体系的にきちんと理解しながら学習したい人におすすめ!基本情報技術者試験の定番テキストの改訂版。 |
| 基本情報技術者 超効率の教科書+よく出る問題集 | 動画でスムーズに学習スタート、テキストでしっかり理解度を深める!よく出る問題を反復学習することで、合格に直結するチカラが身に付く! |