ド・モルガンの法則
ド・モルガンの法則とは、次のような式が成り立つという法則のことです。
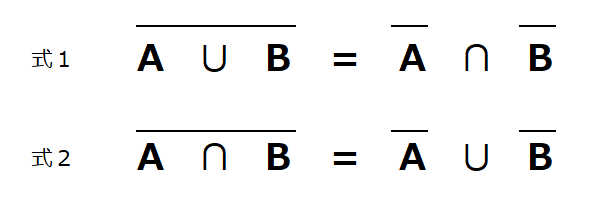

数学者オーガスタス・ド・モルガン(Augustus de Morgan)という人が発見した法則のため「ド・モルガンの法則」と呼ばれています。
それでは、実際にベン図を使って「ド・モルガンの法則」を説明していきます。
ド・モルガンの法則その1「 A ⋃ B = A ⋂ B 」
まずは「A ⋃ B」をベン図であらわします。
「A ⋃ B」(A または B)のベン図は次のとおり。
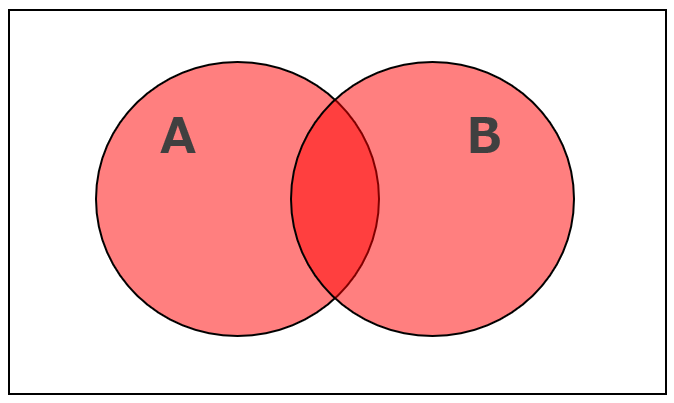
この「A ⋃ B」の否定が「A ⋃ B」です。
「A ⋃ B」(A または Bではない)のベン図は次のとおり。
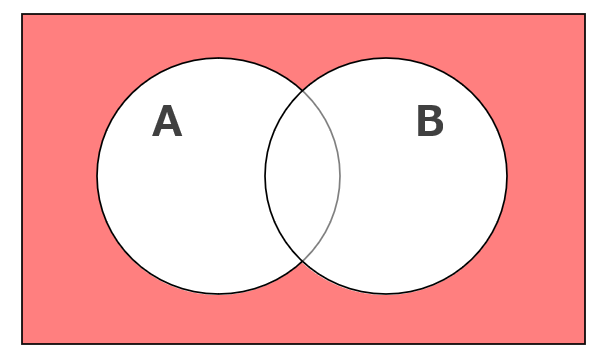
続いては「A ⋂ B」をベン図であらわします。
Aの否定「A」(Aではない)とBの否定「B」(Bではない)のベン図は次のとおり。
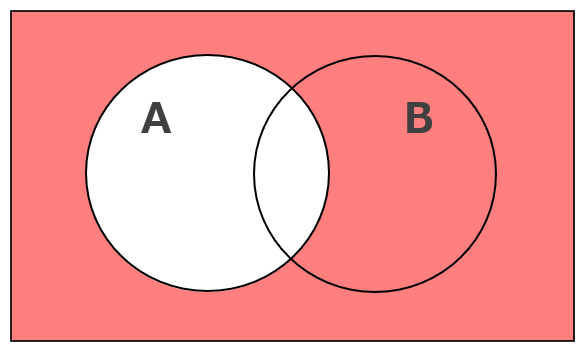
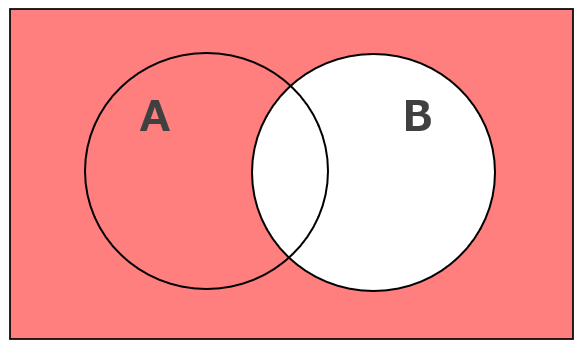
この両方を満たすのが「A ⋂ B」(Aではない かつ Bではない)であり、ベン図は次のとおり。

上記より「A ⋃ B」と「A ⋃ B」はどちらも同じベン図になることがわかります。
このことから「A ⋃ B = A ⋂ B」の式は成り立つといえます。
ド・モルガンの法則その2「 A ⋂ B = A ⋃ B 」
まず「A ⋂ B」をベン図であらわします。
「A ⋂ B」(A かつ B)のベン図は次のとおり。
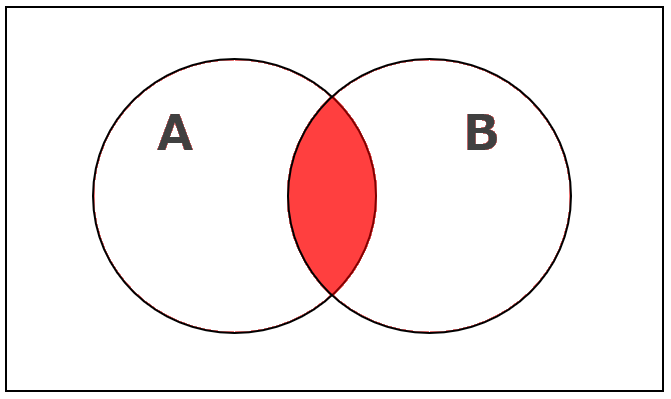
この「A ⋂ B」の否定が「A ⋂ B」です。
「A ⋂ B」(A かつ Bではない)のベン図は次のとおり。
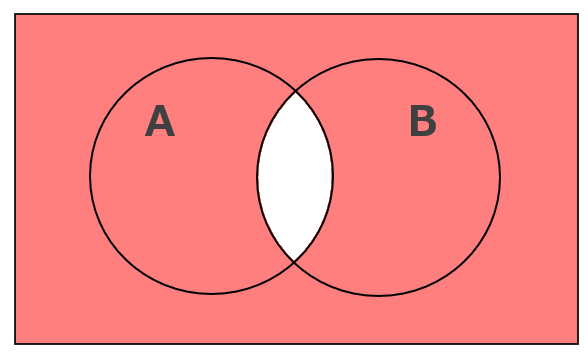
続いては「A ⋃ B」をベン図であらわします。
Aの否定「A」(Aではない)とBの否定「B」(Bではない)のベン図は次のとおり。


このどちらか一方でも満たすのが「A ⋃ B」(Aではない または Bではない)であり、ベン図は次のとおり。

上記より「A ⋂ B = A ⋃ B」はどちらも同じベン図になることがわかります。
このことから「A ⋂ B = A ⋃ B」の式は成り立つといえます。
helpful
この記事は役に立ちましたか?

