
今回のテーマは、ITパスポート試験で時々出題される「確率」についてです。

学生時代に勉強したけど、忘れたなぁ...
確率
確率とは、ある事象が発生する可能性の度合いを数値で表現したものです。
確率は次の式で求められます。

場合の数とは、ある事柄に対して、全部で何通りの場合があるかを示します。
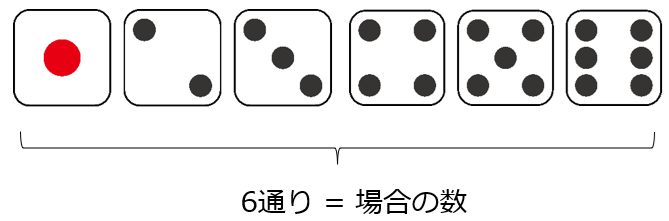
例えば、サイコロを1回振るときの「場合の数」は、出目が1~6なので、6通りです。
なので、サイコロを振って「5」がでる確率は1/6です。(求める場合の数は1、すべての場合の数は6)
確率の積の法則
複数の事象が同時に起こる場合の数を考えるときは、掛け算を使います。
例えば、サイコロを2回投げるとき、1回目に偶数の目が出て、なおかつ2回目に「6」が出る確率は次のように求めます。
- 1回目に偶数の目がでる確率 = 3/6 = 1/2
- 2回目に「6」がでる確率 = 1/6
両方の事象が同時に起こる確率 = 1/2 × 1/6 = 1/12
スポンサーリンク
確率の和の法則
複数の事象が別々に起こる場合の数を考えるときは、足し算を使います。
例えば、サイコロを2回投げるとき、1回目に偶数の目が出る または 2回目に「6」が出る確率は次のように求めます。
- 1回目に偶数の目がでる確率 = 3/6 = 1/2
- 2回目に「6」がでる確率 = 1/6
両方の事象が別々に起こる確率 = 1/2 + 1/6 = 2/3
順列
順列とは、n個の中からr個を順番に取り出して並べる場合の数のことです。
順列は次の式で求められます。

例えば、5個(①,②,③,④,⑤)の中から3個取り出すときの順列を求めてみましょう。

nの数から始めて、1ずつ引いて、rの数だけ掛けていきます。
その結果、次のように求められます。
5P3 = 5 × 4 × 3 = 60通り
組み合わせ
組み合わせとは、n個の中から並び順を考慮せずに r個取り出す場合の数のことです。
組み合わせは次の式で求められます。
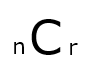
例えば、5個(①,②,③,④,⑤)の中から3個取り出すときの組み合わせを求めてみましょう。
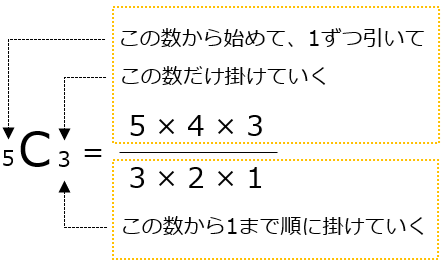
分母は、rの数から1まで順に掛けていき、分子は、nの数から始めて、1ずつ引いて、rの数だけ掛けていきます。
その結果、次のように求められます。
5C3 = 5 × 4 × 3 / 3 × 2 × 1 = 10通り
スポンサーリンク
練習問題
ITパスポート令和6年 問83
1の目がでる確率は1/6なので、1の目がでない確率は5/6です。
複数の事象が同時に起こる場合の数を考えるときは、掛け算を使う(積の法則)ので、次の式で求められます。
3回とも1の目がでない確率 = 5/6 × 5/6 × 5/6 = 125/216

「エ」が正解です。
ITパスポートおすすめの参考書・問題集
| いちばんやさしい ITパスポート | 試験に合格することを目的に企画・構成された対策本。ITの知識がまったくない、未経験者やでもスラスラと学習を進めることができるよう、丁寧に解説。 |
| ITパスポート超効率の教科書 | スキマ時間で効率的にITパスポートの試験対策ができる対策本。動画とテキスト、小テストと過去問を組み合わせた、効果的な4ステップ学習で、合格へと導く。 |
| かやのき先生のITパスポート教室 | ITパスポート受験者のためのやさしいオールインワンタイプの参考書&問題集。イラストや豊富な図解・例え話を駆使して理解しやすく・記憶に残りやすいように説明。 |
| かんたん合格ITパスポート過去問題集 | 信頼と実績の過去問題集。ITパスポート試験合格を最短で目指す人は必携の1冊! |
| 出るとこだけ!ITパスポート | 「ITパスポート」に効率よく合格したい人のため対策本。フルカラーで見やすく「出るとこだけ」を効率的に学習できる1冊! |
| キタミ式イラストIT塾 ITパスポート | すべての解説をイラストベースで行っているため,とてもわかりやすい解説本。いちばん最初に読むITパスポート試験関連の書籍を探している人におすすめ! |

