目次
ハフマン符号化
ハフマン符号化とは、1952年にデビッド・ハフマン(David Albert Huffman)氏によって開発された符号で、データの可逆圧縮などに使用されるものです。

符号化とは
符号化とは、データを「0」と「1」の2進数に置き換えることです。
コンピュータが扱う最小単位のことをビット(bit)といい、1ビットで表現できる数字は「0」と「1」の2つだけです。この「0」と「1」という2個の数字で数をあらわすのが2進数です。
そのため、コンピュータに処理をさせるにはデータを2進数に変換する必要があります。この作業が符号化です。
例えば「ABCD」という文字を次のような2ビットのデータに置き換えるものとします。
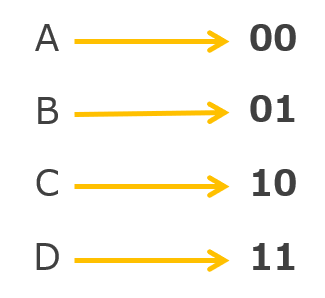
その場合「ABC」という文字は「000101」に置き換えることができます。これが符号化です。

ただし、符号化には処理効率の面からできるだけ少ないビット数で2進数へ変換することが求められます。データ量が少なくなれば、その分メモリの使用量が減り処理を高速に処理することができます。
符号化の作業で、できるだけ少ないビット数で2進数へ変換する方法の1つがハフマン符号化です。
スポンサーリンク
ハフマン符号化とは
ハフマン符号化とは、データの出現頻度に着目した圧縮方法です。
例えば「ABAAACBDBA」という文字列を下記表のルールで符号化すると「00010000001001110100」です。(20ビット ※圧縮しない場合)
| 文字 | 符号 |
| A | 00 |
| B | 01 |
| C | 10 |
| D | 11 |
これに対して「ABAAACBDBA」という文字列を下記表のハフマン符号化で圧縮すると「01000011010111100」の17ビット(※ハフマン符号化で圧縮した場合)となり、今回の例では85%の圧縮率です。(圧縮率は文字の出現頻度により変わる)
| 文字 | 出現頻度 | 符号 |
| A | 5回 | 0 |
| B | 3回 | 10 |
| C | 1回 | 110 |
| D | 1回 | 111 |

ハフマン符号化の手順
ハフマン符号化では、ハフマン木と呼ばれる木構造を用いて符号化します。

[手順1] 各データを出現頻度の高いに並べる
まずは各データを出現頻度の高い順に並べます。
今回の例では「ABAAACBDBA」のデータをハフマン符号化で符号化します。Aが5回、Bが3回、CとDが1回出現しているので、出現頻度の高い順(A、B、C、D)に並べます。

[手順2] 最も出現頻度の低い2つを1つにする
出現頻度の高い順に並べた後は、最も出現頻度の低い2つをつなぐ「親」を作り1つにします。
今回の例では「C」と「D」が最も出現頻度が低いので、2つを繋ぐ「親CD」を作ります。
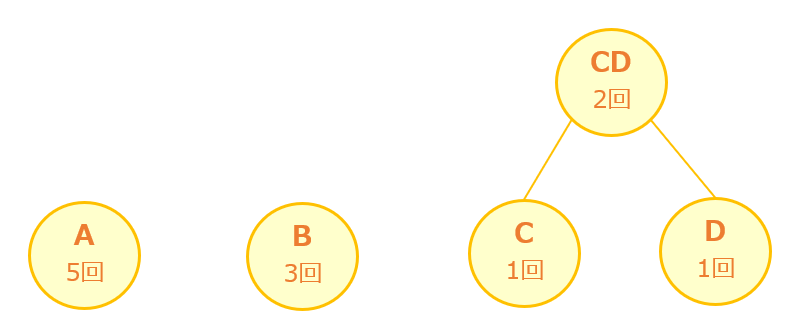
[手順3] 手順2を繰り返して木構造を完成させる
次に最も出現頻度が低い2つは「B」と「CD」なので、「B」と「CD」をつなぐ「親BCD」を作ります。
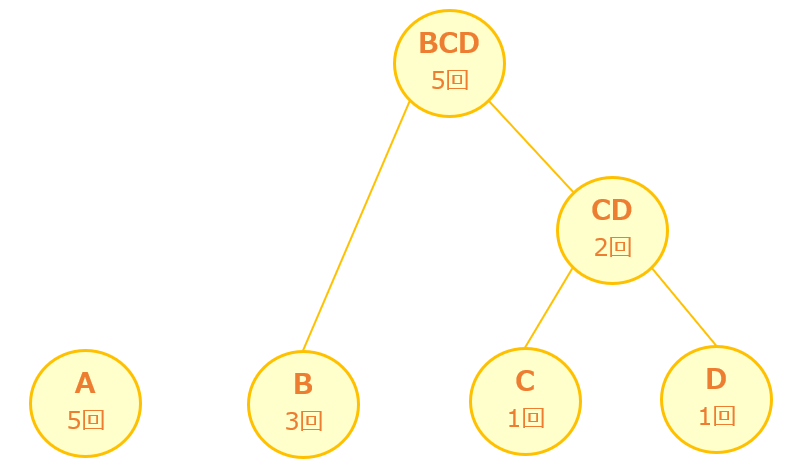
次に最も出現頻度が低い2つは「A」と「BCD」なので、「A」と「BCD」をつなぐ「親ABCD」を作ります。
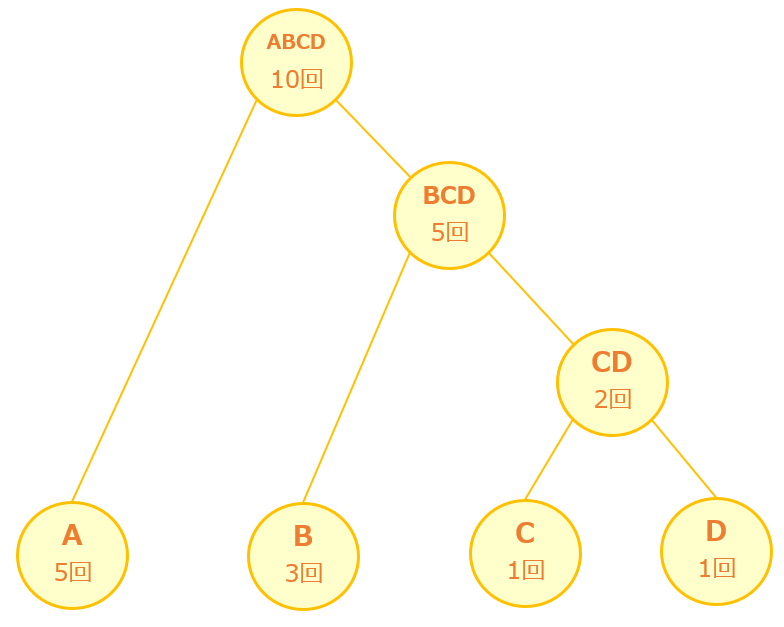
これ以上つなぐものがないので終了です。

[手順4] 作成した木構造に「0」と「1」を割り振る
最後に作成した木構造に「0」と「1」を割り振ります。今回の例では左に「0」、右に「1」を割り振っています。(左に「1」、右に「0」でもOK)
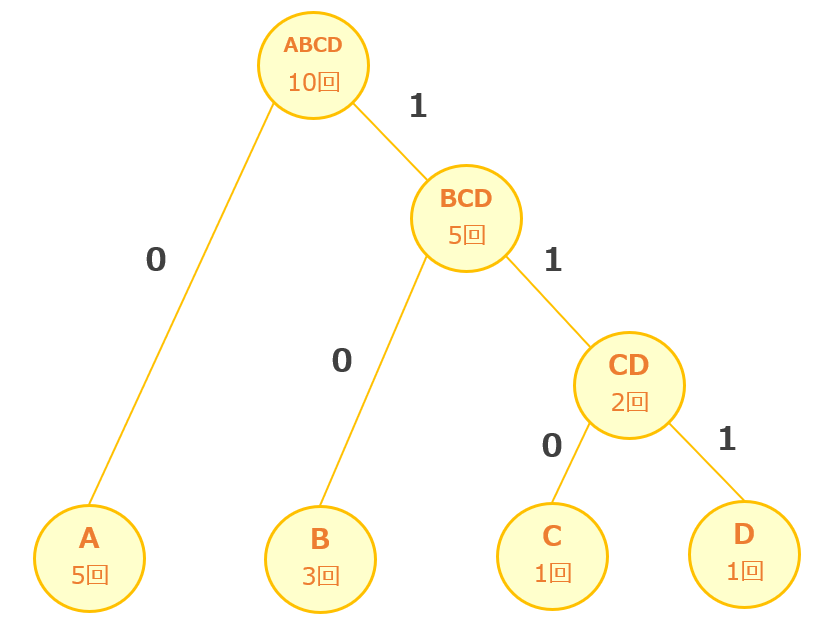
[手順5] 木構造から文字と符号の対応表を作る
手順1~手順4で作成した木構造を上から順にたどっていくことで、下記のような文字と符号の対応表を作成することができます。
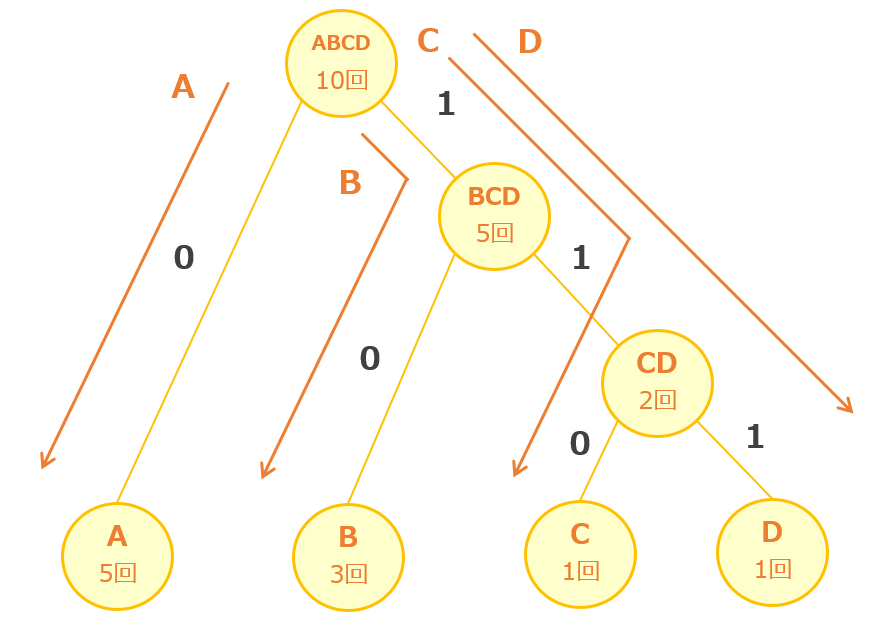
- Aは「ABCD」→「A」なので「0」
- Bは「ABCD」→「BCD」→「B」なので「10」
- Cは「ABCD」→「BCD」→「CD」→「C」なので「110」
- Dは「ABCD」→「BCD」→「CD」→「D」なので「111」
[文字と符号の対応表]
| 文字 | 出現頻度 | 符号 |
| A | 5回 | 0 |
| B | 3回 | 10 |
| C | 1回 | 110 |
| D | 1回 | 111 |
この対応表どおりに符号化すると「ABAAACBDBA」という文字列を「01000011010111100」に変換することができます。
まとめ
- 符号化とはデータを「0」と「1」の2進数に変換すること
- ハフマン符号化はデータの出現頻度に着目して、できるだけ少ないビット数で2進数へ変換する方法

