
次の問題は過去に出題された基本情報技術者試験の過去問です。わかるかな?
難しい...

問題
0以外の数値を浮動小数点表示で表現する場合,仮数部の最上位桁が0以外になるように,桁合わせする操作はどれか。ここで,仮数部の表現方法は,絶対値表現とする。
ア:切上げ イ:切捨て ウ:桁上げ エ:正規化
基本情報技術者平成29年春期 午前問2
コンピュータにおける数値表現の1つであり、主に小数点を含む数値を表現するときに利用するのが「浮動小数点数」です。
本記事では「浮動小数点数」について図解で分かりやすく解説していきます。
本記事で学べること
- 浮動小数点数の形式(符号・指数部・仮数部)を理解
- 浮動小数点数の正規化を理解
- 基本情報技術者試験の過去問の解き方を学ぶ
目次
浮動小数点数
浮動小数点数とは、コンピュータにおける数値を表現する方法の一つで、主に小数点を含む数値を表現するときに利用するものです。
スポンサーリンク
浮動小数点数の形式
浮動小数点数は次のように「符号」「指数部」「仮数部」の形式で表現します。※32ビットの例

- 符号:正の数が0、負の数が1
- 指数部:2nのnの部分を2進数表記にした値を格納(負の数の場合は2の補数を使用する)
- 仮数部:正規化した小数点以下の値を格納
浮動小数点数の「仮数部」と「指数部」に入る値のイメージ例は次のとおりです。(仮数部:小数点以下の値が入る、指数部:2nのnを2進数にした値が入る)

正規化
正規化とは、小数点の位置を調整し最上位桁を0以外の値にする作業のことです。
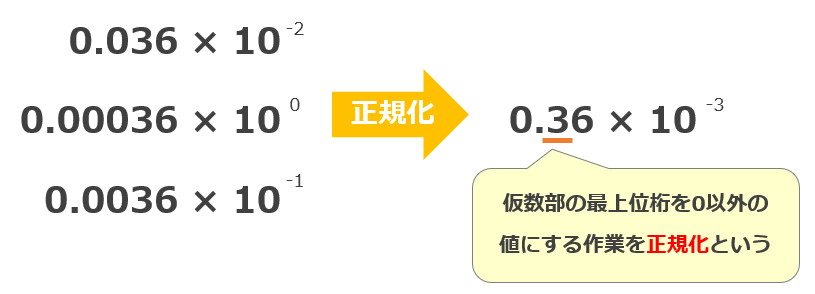

浮動小数点数の仮数部は桁数が決まっており、有効桁数を超えた部分は丸め誤差により切り捨てられてしまいます。
例えば 0.036×102と0.36×101は同じ値です。ただし後者の方が仮数部の桁数は少なくすみます。(前者:036の3桁、後者:36の2桁)
正規化は桁数を稼ぐための作業です。仮数部の最上位桁を0以外に調整することで、丸め誤差が発生する頻度が少なくなり精度が上がります。
浮動小数点数の求め方
例題
10進数の「0.25」を32ビットの浮動小数点数の形式で表現せよ
まずは10進数「0.25」の2進数を求めます。
2進数への変換
- 2 × 0.25 = 0.5
- 2 × 0.5 = 1.0
上記より10進数「0.25」→ 2進数「0.01」
仮数部の求め方
仮数部には2進数「0.01」を正規化した値が入ります。
正規化
0.01
↓ 正規化
0.1 × 2-1
仮数部には次のように正規化で求めた「0.1」の小数点以下の値が入ります。※足りない部分は0で埋める

指数部の求め方
指数部には2nのnを2進数に変換した値が入ります。今回は「0.1 × 2-1」でnは「-1」です。負の数の場合は2の補数を使って2進数を導き出します。
2の補数
0000001 (10進数:1)
↓ すべてのビットを反転させる
1111110
↓ 1を加算する
1111111 (10進数:-1)
指数部には次のように「2-1」の「-1」を2進数に変えた値「1111111」が入ります。

符号を設定して完成
最後に符号を設定すれば完成です。10進数「0.25」は正の数なので、符号には"0"を入れます。(0:正の数、1:負の数)

IEEE754の浮動小数点数
IEEE(米国電気電子学会)により規格化された、浮動小数点数のことを「IEEE754」といいます。
スポンサーリンク
IEEE754 浮動小数点数の形式
IEEE754の浮動小数点数は次の形式で表現します。※32ビットの例

IEEE754の特徴は「1.××」の形で正規化します。例えば、2進数「0.011」を正規化すると0.11 × 2-1だが、IEEE754の場合は、1.1 × 2-2となり1ビット多く保持することができます。(23ビットあれば24ビット分 表現できる)
- 符号:正の数が0、負の数が1
- 指数部:2nのnの部分に127(バイアス)を加算後、2進数表記にした値を格納
- 仮数部:1.××の形式で正規化した小数点以下の値を格納
IEEE754 浮動小数点数の求め方
例題
10進数の「0.375」を32ビットの浮動小数点数(IEEE754)の形式で表現せよ
まずは10進数「0.375」を2進数に変換します。
2進数への変換
- 2 × 0.375 = 0.75
- 2 × 0.75 = 1.5
- 2 × 0.5 = 1.0
上記より10進数「0.375」→ 2進数「0.011」
仮数部の求め方(IEEE754)
仮数部には2進数「0.011」を1.××形式に正規化した値が入ります。
正規化
0.011
↓ 正規化
1.1 × 2-2
仮数部には次のように正規化で求めた「1.1」の小数点以下の値が入ります。※足りない部分は0で埋める

指数部の求め方(IEEE754)
指数部には2nのnにバイアスと呼ばれる127を加算した結果を2進数に変換した値が入ります。
バイアスには「ゲタをはかせる」(ゲタ履き表現)という意味があり、指数部にバイアスを加算することで、負の数を含む表現が正の数だけであらわせるようになります。
今回の例では、「1.1 × 2-2」とnの部分が「-2」なので「-2」にバイアスの「127」を加算します。
バイアスを加算
-2 + 127 = 125
↓ 2進数に変換
01111101
バイアス値を加算した結果である「125」を2進数に変えた値「01111101」が指数部に入ります。

符号を設定して完成(IEEE754)
最後に符号を設定すれば完成です。10進数「0.375」は正の数なので、符号には"0"を入れます。(0:正の数、1:負の数)

基本情報技術者試験 過去問の解説
問題
0以外の数値を浮動小数点表示で表現する場合,仮数部の最上位桁が0以外になるように,桁合わせする操作はどれか。ここで,仮数部の表現方法は,絶対値表現とする。
ア:切上げ イ:切捨て ウ:桁上げ エ:正規化
基本情報技術者平成29年春期 午前問2
浮動小数点数の正規化は、仮数部と指数部を調整することで仮数部の最上位桁を0以外の値にする作業です。正規化の目的は、有効桁数を最大化し丸め誤差をできるだけ少なくすることです。

基本情報技術者試験おすすめの参考書・問題集
| いちばんやさしい 基本情報技術者 | 『基本情報技術者試験』試験に、短期間で一発合格するための試験対策本。ITの知識がまったくない、未経験者やでもスラスラと学習を進められるよう、丁寧に解説。 |
| かやのき先生の基本情報技術者教室 | 基本情報技術者をめざす方のためのやさしいオールインワンタイプの参考書&問題集。イラストや豊富な図解・例え話を駆使して理解しやすく・記憶に残りやすいように説明。 |
| 基本情報技術者 パーフェクトラーニング過去問題集 | 科目A・Bともに万全の対策ができる、定番の過去問題集!科目A・科目Bの両方について万全の対策ができる。 |
| キタミ式イラストIT塾 基本情報技術者 | すべての解説をイラストベースで行っているため,とてもわかりやすい解説本。いちばん最初に読む基本情報技術者試験関連の書籍を探している人におすすめ! |
| 出るとこだけ!基本情報技術者[科目B] | 基本情報技術者【科目B】対策の定番書!前提知識+解き方+試験問題を掲載。効率よく学習できる。 |
| 基本情報技術者 合格教本 | 出題範囲を体系的にきちんと理解しながら学習したい人におすすめ!基本情報技術者試験の定番テキストの改訂版。 |
| 基本情報技術者 超効率の教科書+よく出る問題集 | 動画でスムーズに学習スタート、テキストでしっかり理解度を深める!よく出る問題を反復学習することで、合格に直結するチカラが身に付く! |

