
次の問題は基本情報技術者試験で過去に出題された「2の補数」についての問題です。解けるかな?

問題
8ビットの2進数11010000を右に2ビット算術シフトしたものを,00010100から減じた値はどれか。ここで,負の数は2の補数表現によるものとする。
- ア:00001000
- イ:00011111
- ウ:00100000
- エ:11100000
基本情報技術者平成24年秋期 午前問1
問題
ある整数値を,負数を2の補数で表現する2進表記法で表すと最下位2ビットは"11"であった。10進表記法の下で,その整数値を4で割ったときの余りに関する記述として,適切なものはどれか。ここで,除算の商は,絶対値の小数点以下を切り捨てるものとする。
- ア:その整数値が正ならば3
- イ:その整数値が負ならば-3
- ウ:その整数値が負ならば3
- エ:その整数値の正負にかかわらず0
基本情報技術者平成30年春期 午前問1
コンピュータで負の数をあらわすのに使用する「2の補数」、「2の補数」は理解してしまえば、そこまで難しい言葉ではありません。しかし、基本情報技術者試験では単純に「2の補数」を求めるだけの問題が出題されることもありますが、上記の過去問のようにそうではないことも多いです。
本記事では「2の補数」について図解で分かりやすく解説していきます。
本記事で学べること
- 2の補数の求め方を理解
- 基本情報技術者試験の過去問の解き方を学ぶ
目次
2の補数
補数とは「補う数」という意味で「足すと桁が1つ上がる数のうち最も小さい数」のことを「基数の補数」といいます。

スポンサーリンク
例えば、10進数の「4」という数に「6」を足すと、桁が1つ上がり「10」となり「6」は「4」に対する「10の補数」です。
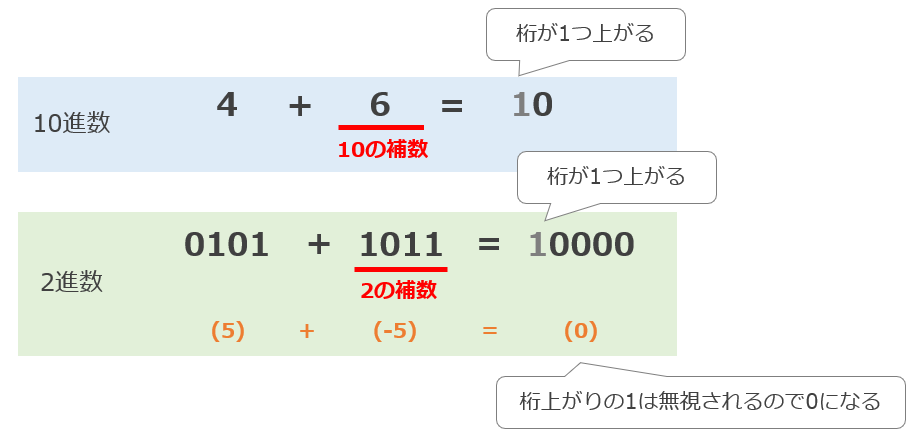
2進数も同じで「0101」に「1011」を足すと、桁が1つ上がり「10000」となり「1011」は「0101」に対する「2の補数」であるのがわかります。
コンピュータでは、負の数をあらわすのに「2の補数」を使用しています。
2の補数の最上位ビットは符号(0:正の数、1:負の数)として扱うことができます。この正の数と負の数はお互いに2の補数という関係にあります。(例えば、正の数「0100(4)」の2の補数は負の数「1100(-4)」であり、負の数「1100(-4)」の2の補数は正の数「0100(4)」となる)
2の補数の求め方
例題
2進数「0101」に対する「2の補数」を求めよ
2の補数は次のような手順で求めることができます。
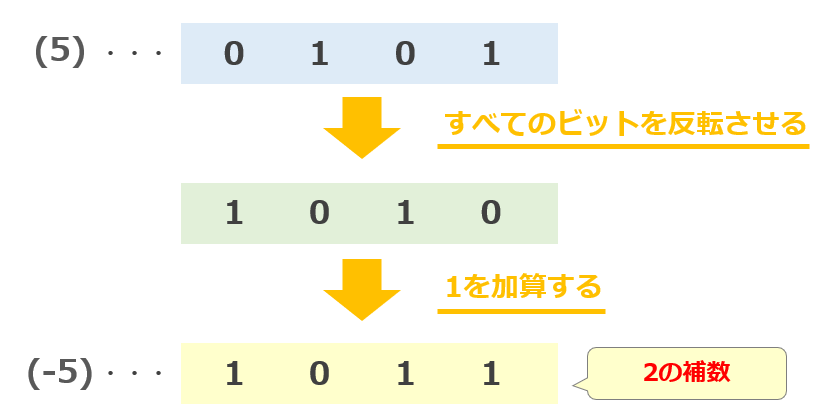
【手順1】すべてのビットを反転させる
0101 (10進数:5)
↓ すべてのビットを反転させる
1010
【手順2】反転させたビットに1を加算する
1010 + 0001 = 1011(10進数:-5)
2の補数を使った計算
例題
「5 - 3」を2進数を使い計算せよ。
それでは、2の補数を使った計算方法の例を紹介します。例題のように2の補数を使って減法する場合は「5 - 3」を「5 + (-3)」として計算します。
まずは「5」と「3」を2進数にします。※8ビットを例としています。
10進数「5」→ 2進数「0000 0101」
10進数「3」→ 2進数「0000 0011」
そして「3」に対する2の補数を求めます。
0000 0011 (3)
↓ すべてのビットを反転させる
1111 1100
↓ 1を加算する
1111 1101 (-3)
最後に「0000 0101」(5) + 「1111 1101」(-3) を計算します。計算式と答えは次のとおりです。


基本情報技術者試験 過去問の解説
スポンサーリンク
基本情報技術者平成24年秋期 午前問1
問題
8ビットの2進数11010000を右に2ビット算術シフトしたものを,00010100から減じた値はどれか。ここで,負の数は2の補数表現によるものとする。
- ア:00001000
- イ:00011111
- ウ:00100000
- エ:11100000
基本情報技術者平成24年秋期 午前問1
この問題は次の2つのステップをおこなうことで答えを求めることができます。
- ステップ1:2進数11010000を右に2ビット算術シフトした値を求める
- ステップ2:「00010100 - ステップ1で求めた値」を計算する
【ステップ1】右に2ビット算術シフトした値を求める
まずは2進数11010000を右に2ビット算術シフトします。算術シフトとは割り算をおこなうということです。右に2ビットシフトすると元の数を1/22倍にした値を得ることができます。
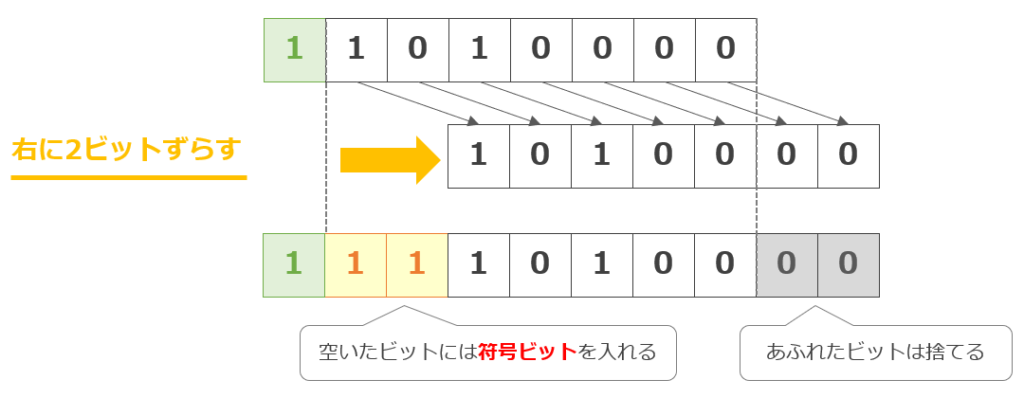
算術シフト
11010000
↓ 先頭の符号ビット以外の桁を右に2ビットずらす
11110100 00
(あふれたビットは捨てて、空いたビットに符号ビットを入れる)
算術シフトの詳細はこちら
2進数「11010000」を右に2ビット算術シフトした結果、2進数「11110100」を求めることができました。
【ステップ2】「00010100 - ステップ1で求めた値」を計算する
ステップ1で求めた値を「x」とすると、次のように式を変換して計算します。
- xが正の数の場合は「00010100 - x」を「00010100 + (-x)」として計算。※「3 - (1)」を「3 + (-1)」に変えて計算するのと同じ
- xが負の数の場合は「00010100 - (-x)」を「00010100 + x」として計算。※「3 - (-1)」を「3 + 1」に変えて計算するのと同じ
問題文の中に「負の数は2の補数表現によるものとする」と書かれているので、ステップ1で求めた値が負の数であることがわかります。(先頭のビットが"1"なので負の数)
xが負の数の場合は「00010100 - (-x)」を「00010100 + x」として計算するので、ステップ1で求めた値の2の補数を求めます。(負の数の2の補数を求めることで正の数に変換できる)
2の補数を求める
11110100
↓ すべてのビットを反転させる
00001011
↓ 1を加算する
00001100
あとは、「00010100 + 00001100」を計算することで答えを求めることができます。


ちなみに次のように求めることもできます。
10進数で計算する方法
(1) 2進数「00010100」→ 10進数「20」・・・ ①
(2) ステップ1で求めた2進数「11110100」の2の補数を求めると「00001100」(10進数:12)になるため2進数「11110100」の10進数は以下になる
2進数「11110100」は10進数の「-12」・・・②
(3)「① - ②」 を10進数で計算する
20 - (-12) = 32 ・・・③
(4) ③の計算結果を2進数に戻す
00100000
基本情報技術者平成30年春期 午前問1
問題
ある整数値を,負数を2の補数で表現する2進表記法で表すと最下位2ビットは"11"であった。10進表記法の下で,その整数値を4で割ったときの余りに関する記述として,適切なものはどれか。ここで,除算の商は,絶対値の小数点以下を切り捨てるものとする。
- ア:その整数値が正ならば3
- イ:その整数値が負ならば-3
- ウ:その整数値が負ならば3
- エ:その整数値の正負にかかわらず0
基本情報技術者平成30年春期 午前問1
この問題は次の2つのステップをおこなうことで答えを求めることができます。
- ステップ1:正の整数で計算(正の整数 ÷ 4)
- ステップ2:負の整数で計算(負の整数 ÷ 4)
[ステップ1] 正の整数で計算(正の整数 ÷ 4)
最下位2ビットが“11”である正の整数で計算します。今回は2進数「0011」で計算してみます。
整数値が正
2進数「0011」→ 10進数「3」
10進数「3」を「4」で割ったときの余りは「3」
[ステップ2] 負の整数で計算(負の整数 ÷ 4)
最下位2ビットが“11”である負の整数で計算します。今回は2進数「1011」(負の数なので先頭ビットは1)で計算してみます。
まずは「1011」の10進数が知りたいので、2の補数を求めます。
2の補数を求める
1011
↓ すべてのビットを反転させる
0100
↓ 1を加算
0101 (10進数:5)
2の補数を求めた結果、2進数「1011」は10進数で「-5」であることがわかりました。負の整数がわかったので「負の整数 ÷ 4」の式を解きます。
式
-5 ÷ 4 = -2 余り 3
もしくは
-5 ÷ 4 = -1 余り -1
負数を4で割ると余りは「3」 または「-1」になることがわかります。(※余りにマイナスを許容するかしないかで変わる)
ここで、設問の「除算の商は,絶対値の小数点以下を切り捨てるものとする」という条件を適用します。
式
-5 ÷ 4 = -1.25
↓ 絶対値の小数点以下を切り捨てると商は「-1」
商が「-1」ならば余りは「-1」


シフト演算を使った解き方
4で割ったときの余りを求めるので、右算術シフトで右へ2ビットシフト(4は22になる)します。右算術シフトでは、あふれたビットが割り算の余り(わり切れるときは"0"があふれる、わり切れないときは"1"があふれる)を示します。
[整数値が正の場合]
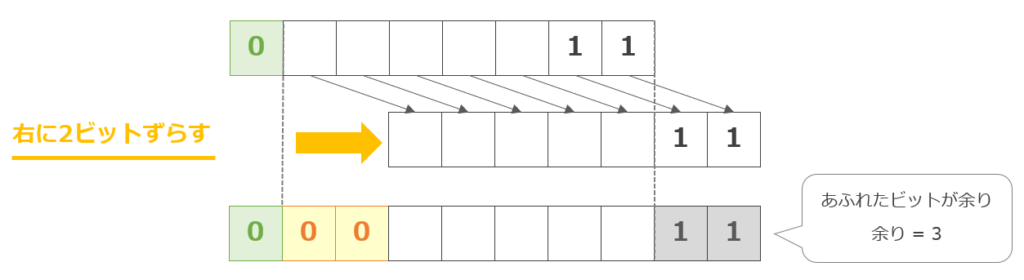
[整数値が負の場合]

上記図のように、整数値が正の場合は「11」があふれるので余りは「3」、整数値が負の場合も同様に「11」があふれ、負の数なので2の補数で値を求めると余りは「-1」と導き出すことができます。
基本情報技術者試験おすすめの参考書・問題集
| いちばんやさしい 基本情報技術者 | 『基本情報技術者試験』試験に、短期間で一発合格するための試験対策本。ITの知識がまったくない、未経験者やでもスラスラと学習を進められるよう、丁寧に解説。 |
| かやのき先生の基本情報技術者教室 | 基本情報技術者をめざす方のためのやさしいオールインワンタイプの参考書&問題集。イラストや豊富な図解・例え話を駆使して理解しやすく・記憶に残りやすいように説明。 |
| 基本情報技術者 パーフェクトラーニング過去問題集 | 科目A・Bともに万全の対策ができる、定番の過去問題集!科目A・科目Bの両方について万全の対策ができる。 |
| キタミ式イラストIT塾 基本情報技術者 | すべての解説をイラストベースで行っているため,とてもわかりやすい解説本。いちばん最初に読む基本情報技術者試験関連の書籍を探している人におすすめ! |
| 出るとこだけ!基本情報技術者[科目B] | 基本情報技術者【科目B】対策の定番書!前提知識+解き方+試験問題を掲載。効率よく学習できる。 |
| 基本情報技術者 合格教本 | 出題範囲を体系的にきちんと理解しながら学習したい人におすすめ!基本情報技術者試験の定番テキストの改訂版。 |
| 基本情報技術者 超効率の教科書+よく出る問題集 | 動画でスムーズに学習スタート、テキストでしっかり理解度を深める!よく出る問題を反復学習することで、合格に直結するチカラが身に付く! |

