

問題
8ビットのビット列の下位4ビットが変化しない操作はどれか。
- ア:16進表記 0F のビット列との排他的論理和をとる。
- イ:16進表記 0F のビット列との否定論理積をとる。
- ウ:16進表記 0F のビット列との論理積をとる。
- エ:16進表記 0F のビット列との論理和をとる。
基本情報技術者平成28年秋期 午前問1
真(true:条件が成立)と偽(false:条件が成立しない)という2つの値を用いて行う演算である論理演算は、基本情報技術者試験や応用情報技術者試験で出題される問題です。
論理演算には「論理積」(AND)、「論理和」(OR)、「否定」(NOT)、排他的論理和(XOR)などがあります。
本記事では、論理演算について図解で分かりやすく解説しています。
本記事で学べること
- 論理演算(論理和・論理積・否定・排他的論理和)を理解
- 基本情報技術者試験の過去問の解き方を学ぶ
目次
論理積(AND)
論理積(AND)とは、2つある条件がともに"真"(true:条件が成り立つ)のときのみ"真"(true)を出力する演算です。
「AかつB」と表現し、論理演算記号では(A・B)または(A∧B)という記号で表現します。
スポンサーリンク
論理積のベン図

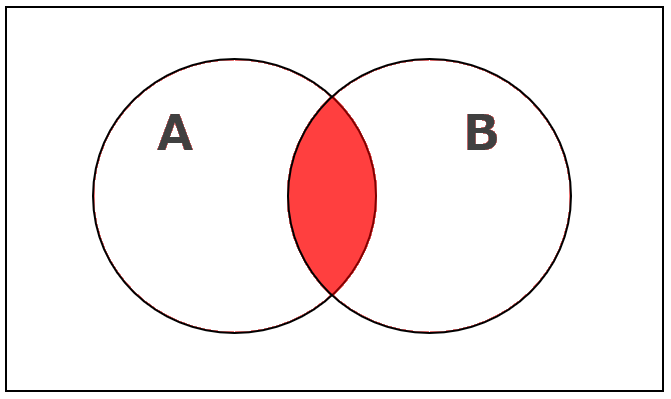
論理積は、AとBの両方にあてはまる場合に"真"(true)を出力します。ベン図で赤くなっている部分が"真"(true)を返す条件です。
例
A:サッカーチームに所属、B:野球チームに所属
サッカーチームに所属 かつ 野球チームに所属 している場合に"真"(true)、それ以外は"偽"(false)を出力する。
論理積の真理値表
論理積の真理値表は次のとおりです。

| A | B | A・B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
論理積では、AとBの両方が"1"(true)の場合のみ"1"(true)を出力し、それ以外は"0"(false)を出力します。
論理和(OR)
論理和(OR)とは、2つある条件のいずれかが"真"(true:条件が成り立つ)である場合に"真"(true)を出力する演算です。
「AまたはB」と表現し、論理演算記号では(A+B)または(A∨B)という記号で表現します。
論理和のベン図
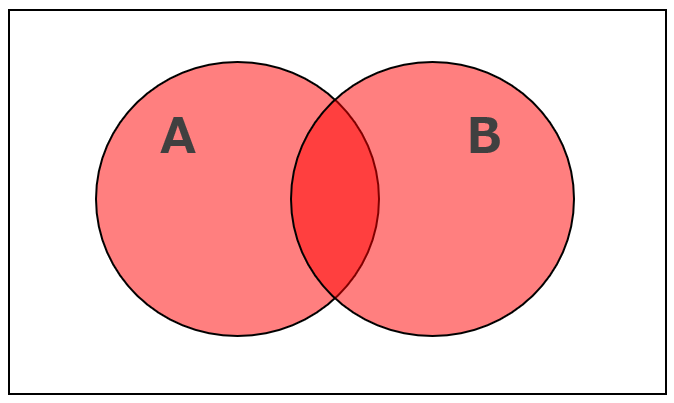
論理和は、AとBのどちらか もしくは 両方にあてはまる場合に"真"(true)を出力します。ベン図で赤くなっている部分が"真"(true)を返す条件です。
例
A:サッカーチームに所属、B:野球チームに所属
サッカーチームに所属 または 野球チームに所属 している場合に"真"(true)、どちらにも所属していない場合は"偽"(false)を出力する。
論理和の真理値表
論理和の真理値表は次のとおりです。
| A | B | A+B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
論理和では、AとBのどちらか もしくは 両方が"1"(true)の場合に"1"(true)を出力し、それ以外は"0"(false)を出力します。
否定(NOT)
否定(NOT)とは、1つの条件に対して、真偽値の値を反転させる演算です。
「Aではない」と表現し、論理演算記号では(A)(もしくは¬)という記号で表現します。
否定のベン図
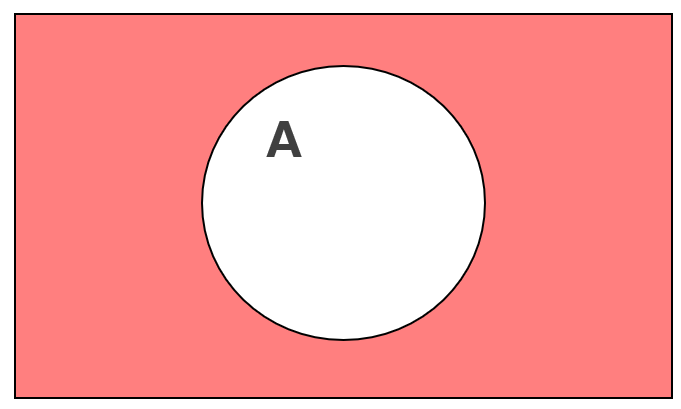
否定はAではないときに"真"(true)を出力します。ベン図で赤くなっている部分が"真"(true)を返す条件です。
否定の真理値表
否定の真理値表は次のとおりです。
| A | (A) |
| 0 | 1 |
| 1 | 0 |
否定はAが"0"(false)の場合に"1"(true)を出力し、Aが"1"(true)の場合に"0"(false)を出力します。

排他的論理和(XOR)
排他的論理和(XOR)とは、2つある条件のうち片方だけが"真"(true:条件が成り立つ)である場合に"真"を出力する演算です。
論理演算記号では(A⊕B)という記号で表現します。
排他的論理和のベン図
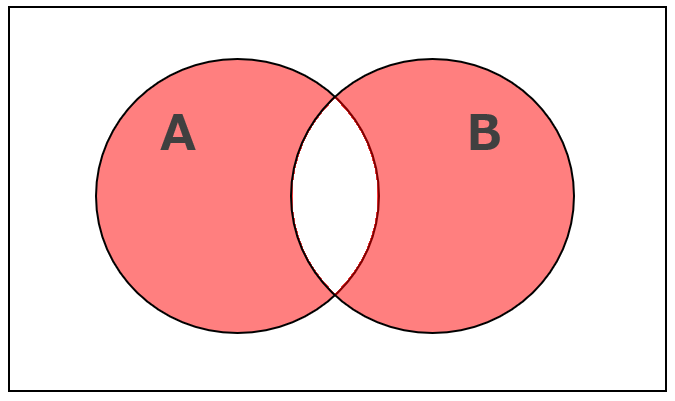
排他的論理和は、AとBのどちらか片方にあてはまる場合に"真"(true)を出力します。ベン図で赤くなっている部分が"真"(true)を返す条件です。
排他的論理和の真理値表
排他的論理和の真理値表は次のとおりです。
| A | B | A⊕B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
排他的論理和では、AとBのどちらか片方が"1"(true)の場合に"1"(true)を出力し、それ以外は"0"(false)を出力します。
スポンサーリンク
基本情報技術者試験 過去問の解説
問題
8ビットのビット列の下位4ビットが変化しない操作はどれか。
- ア:16進表記 0F のビット列との排他的論理和をとる。
- イ:16進表記 0F のビット列との否定論理積をとる。
- ウ:16進表記 0F のビット列との論理積をとる。
- エ:16進表記 0F のビット列との論理和をとる。
基本情報技術者平成28年秋期 午前問1
まずは16進数「0F」を2進数にします。
16進数「0F」→ 2進数「00001111」
※0 → 0000、F → 1111
この値に対して仮の値で論理演算をおこない、仮の値の下位4ビットが変化しない操作を求めます。今回は「00000011」を仮の値とします。
ア:排他的論理和(XOR)
ア:16進表記 0F のビット列との排他的論理和をとる。
排他的論理和
00000011 XOR 00001111 = 00001100
下位4ビットが変化したので「不正解」
※排他的論理和はどちらか片方のみが"1"のときに"1"を返し、それ以外は"0"を返す
イ:否定論理積(NAND)
イ:16進表記 0F のビット列との否定論理積をとる。
否定的論理積
00000011 NAND 00001111 = 11111100
下位4ビットが変化したので「不正解」
※否定的論理積は論理積の否定なので、両方が"1"のときに"0"を返し、それ以外は"1"を返す
ウ:論理積(AND)
ウ:16進表記 0F のビット列との論理積をとる。
論理積
00000011 AND 00001111 = 00000011
下位4ビットが変化しないので「正解」
※論理積は両方が"1"のときに"1"を返し、それ以外は"0"を返す
エ:論理和(OR)
エ:16進表記 0F のビット列との論理和をとる。
論理和
00000011 OR 00001111 = 00001111
下位4ビットが変化しないので「不正解」
※論理和は片方または両方が"1"のときに"1"を返し、それ以外は"0"を返す

基本情報技術者試験おすすめの参考書・問題集
| いちばんやさしい 基本情報技術者 | 『基本情報技術者試験』試験に、短期間で一発合格するための試験対策本。ITの知識がまったくない、未経験者やでもスラスラと学習を進められるよう、丁寧に解説。 |
| かやのき先生の基本情報技術者教室 | 基本情報技術者をめざす方のためのやさしいオールインワンタイプの参考書&問題集。イラストや豊富な図解・例え話を駆使して理解しやすく・記憶に残りやすいように説明。 |
| 基本情報技術者 パーフェクトラーニング過去問題集 | 科目A・Bともに万全の対策ができる、定番の過去問題集!科目A・科目Bの両方について万全の対策ができる。 |
| キタミ式イラストIT塾 基本情報技術者 | すべての解説をイラストベースで行っているため,とてもわかりやすい解説本。いちばん最初に読む基本情報技術者試験関連の書籍を探している人におすすめ! |
| 出るとこだけ!基本情報技術者[科目B] | 基本情報技術者【科目B】対策の定番書!前提知識+解き方+試験問題を掲載。効率よく学習できる。 |
| 基本情報技術者 合格教本 | 出題範囲を体系的にきちんと理解しながら学習したい人におすすめ!基本情報技術者試験の定番テキストの改訂版。 |
| 基本情報技術者 超効率の教科書+よく出る問題集 | 動画でスムーズに学習スタート、テキストでしっかり理解度を深める!よく出る問題を反復学習することで、合格に直結するチカラが身に付く! |

