桁落ちとは

桁落ちを分かりやすく解説

桁落ちとは

桁落ちとは、値がほぼ等しく丸め誤差を持つ数値の差を求めた時に、有効数字（位取りを示すだけのゼロを除いた意味のある数字）が大きく減ることによって生じる誤差のことです。

よくわからない・・・

桁落ちは少し難しいので、例を用いて説明していきます。

スポンサーリンク

桁落ちの計算例

例えば、値がほぼ等しい次の数値の差を求めてみます。※説明のため10進数を例にしています。

まず小数の計算をするため、浮動小数点数にします。

浮動小数点数とは、コンピュータが小数を扱う時に使う方法です。

今回の例ではfloat型を使用します。float型の浮動小数点型変は、有効数字は７桁です。そのため７桁に収まらない数字は、最後の桁で「丸め誤差」が発生します。

丸め誤差とは、コンピュータが表現できる数の範囲（有効桁）を超えてしまった際に「四捨五入」や「切り上げ」「切り捨て」などを行い有効桁以降の値を捨てることにより生じる誤差のことです。

それでは、2つの差を求めてみます。

値がほぼ等しい有効数字が7桁の値の差を求めた結果、有効数字が4桁に減っています。

そして、浮動小数点数なので正規化され、仮数部が７桁になるように不足している部分を0で埋めます。この時付与された「0」は正しい値であるかの保証がないのです。

浮動小数点数の正規化とは、次のイメージのように仮数部の最上位を0以外の値にする作業のことです。

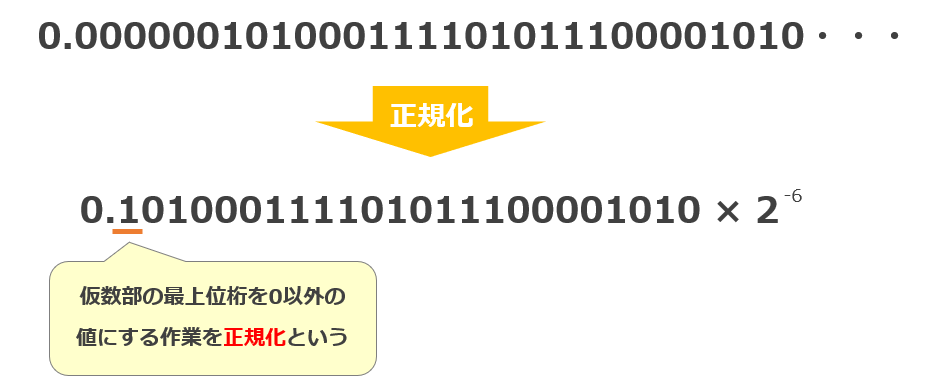
それでは、正規化によって付与された「0」が本当に正しいものではないのか確認してみましょう。

丸め誤差や正規化を考えずに、元となる値の差を計算すると

答えは「0.03165445」です。やはり「0」は正しい値ではありませんでした。

桁落ちによって「0.3165000 × 10の-1乗」となりましたが、本来であれば「0.3165445 × 10の-1乗」が正しい値です。※赤字の部分が桁落ちにより発生した誤差

このように、値がほぼ等しく丸め誤差を持つ数値の差を求めた時に、有効数字が大きく減ることによって生じる誤差のことを「桁落ち」といいます。