目次
レインボーテーブルとは
レインボーテーブル (rainbow table)とは、ハッシュ値から元のデータ(平文)を導き出すための手法で、特殊なテーブルを使用します。
レインボーテーブルは不正入手したハッシュ値(パスワード)の解析などに利用されており、サイバー攻撃の一種です。
スポンサーリンク

ハッシュ関数とは
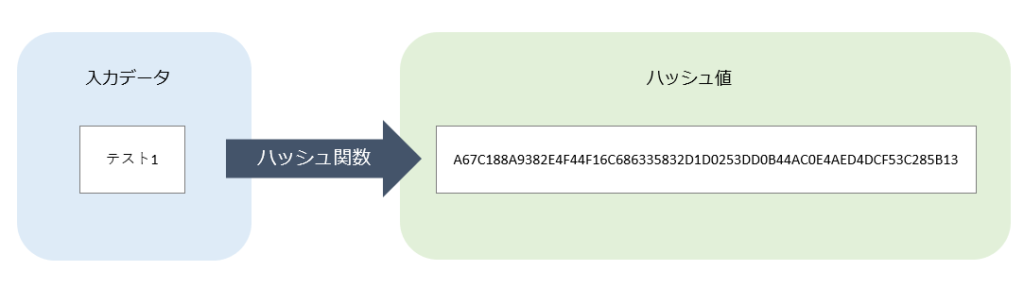
ハッシュ関数とは、入力データを一定の手順で計算を行い、入力値のデータの長さに関わらず、決まった長さの文字列を出力する関数のことです。
ハッシュ関数により得られたデータのことを「ハッシュ値」と呼び、ハッシュ値から元の入力データを推測するのは非常に困難(一方向性関数)といわれています。
この困難な作業を行うのがレインボーテーブルです。
レインボーテーブルで使用する2つの関数
レインボーテーブルでは「ハッシュ関数」と「還元関数」の2つの関数の特性を利用します。それぞれの関数の特性は次の通りです。
ハッシュ関数
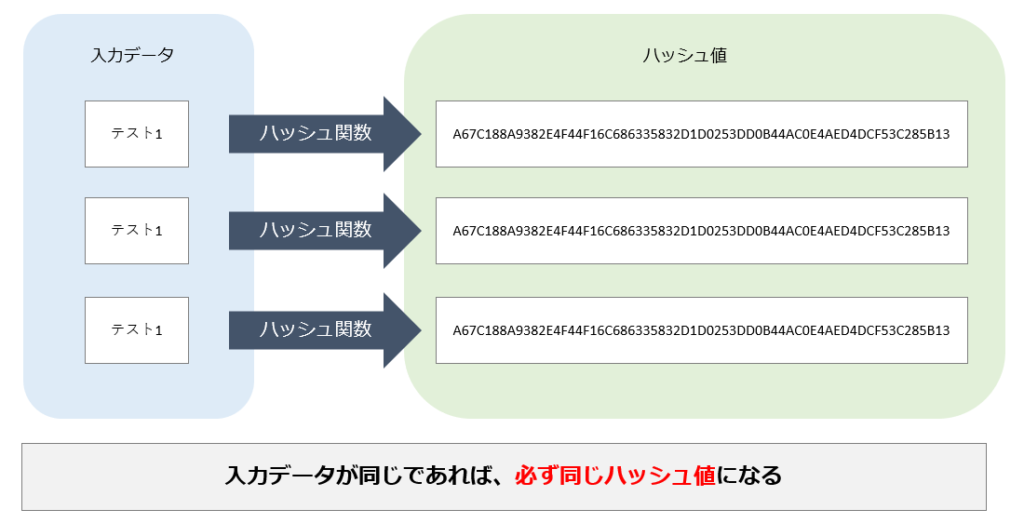
ハッシュ関数には様々な関数(MD5、SHA-1、SHA-2、SHA-3など)が存在します。そのため、「平文」から得られる「ハッシュ値」もハッシュ関数により異なります。
しかし、使用するハッシュ関数と「平文」が決まれば、得られる「ハッシュ値」は必ず同じです。
還元関数
還元関数とは、ハッシュ値から平文候補となる値を生成する関数です。
ハッシュ値は一方向性関数のため、ハッシュ値から元のデータである「平文」を推測することは困難です。そのため、還元関数を利用して平文候補となる値を生成し、元のデータである「平文」を導き出すための手助けをする役割を持ちます。
スポンサーリンク
レインボーテーブルの仕組み
[事前準備] チェーンを作成する(チェーン化)
使用する記憶域の量を削減するために、ハッシュ関数と還元関数を利用し、平文とハッシュ値とのペアを「チェイン化」していきます。
1. 任意の「平文」をハッシュ関数で「ハッシュ値」にする
任意の平文をハッシュ関数でハッシュ値へと変換します。
2. 還元関数で「ハッシュ値」を「平文」に戻す
ハッシュ関数で変換した「ハッシュ値」を、還元関数で「平文」へと戻します。※ここで使用した還元関数は「還元関数1」とします。
3. 再び「平文」をハッシュ関数で「ハッシュ値」にする
循環関数で戻した「平文」をハッシュ関数で再び「ハッシュ値」へと変換します。
4. 再び還元関数で「ハッシュ値」を「平文」に戻す
ハッシュ関数で変換した「ハッシュ値」を、還元関数で再び「平文」へと戻します。そして、3と4の処理を一定回数繰り返し「平文」と「ハッシュ値」とのペアを「チェイン化」していきます。
還元関数は2で使った関数とは異なる関数を使用します。同じ還元関数は使用しないので、チェインの長さ分だけ還元関数を用意するのも特徴です。
※ここで使用した還元関数は「還元関数2」とします。
5. チェイン化した先頭と末尾を記録する
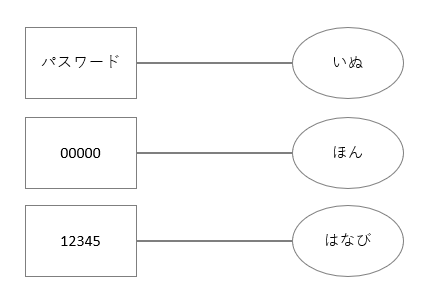
上記の1~4で生成したチェインの先頭と末尾の情報を記録しておきます。(全てを保存しておくと膨大な記憶域が必要なため、記憶域を削減する)
※今回は説明の都合上、還元関数は2回だけ実施した例(チェインの先頭「パスワード」の末尾が「いぬ」)で説明しています。
[攻撃例] ハッシュ値から平文を導き出すまでの流れ
ここからは、不正入手したハッシュ値をレインボーテーブルを利用して元のデータ(平文)を導き出すまでの流れを図解で説明していきます。
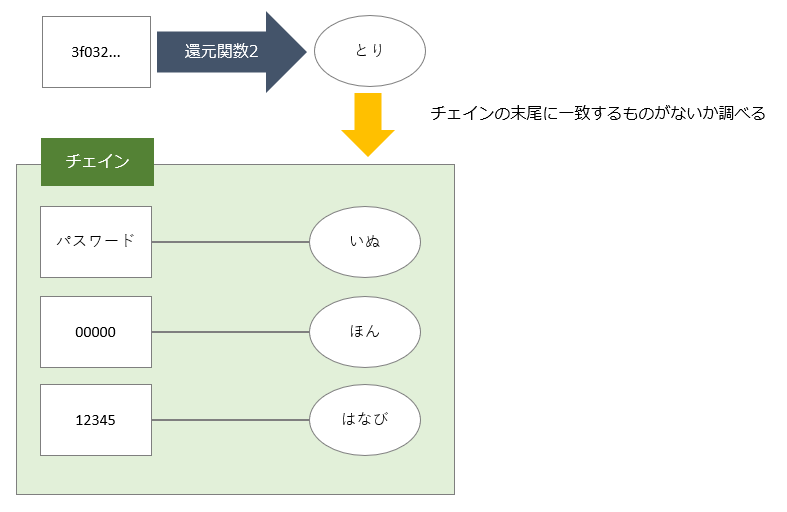
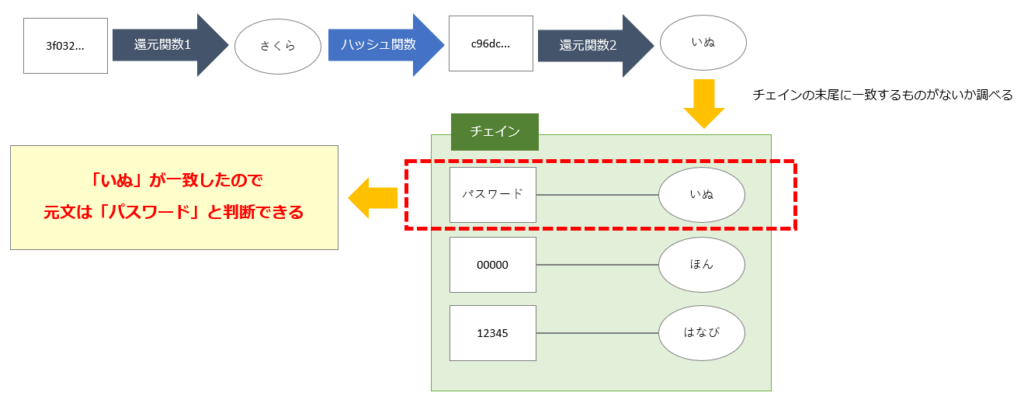
1. 入手したハッシュ値を末尾の還元関数2で「平文」に戻し、記録してある末尾の「平文」と比較する
不正入手した「ハッシュ値」を、チェインの末尾で使用した還元関数2で「平文」に戻します。そして、記録してあるチェインの末尾の「平文」と比較し、一致しているものがないかを調べます。
一致している場合は、一致したチェインの先頭が不正入手した「ハッシュ値」の元のデータ(平文)なので処理は終了です。
一致していない場合は、2の処理へと進みます。

2. 入手したハッシュ値を一つ前の還元関数1で「平文」→「ハッシュ値」→「平文」と変換し、記録してある末尾の「平文」と比較する
不正入手した「ハッシュ値」を、チェインの末尾の一つ前で使用した還元関数1で「平文」に戻します。そして、チェインを作成した手順と同じで「ハッシュ値」へと変換(チェイン作成時の手順3)、還元関数2を使い「平文」へと変換(チェイン作成時の手順4)していきます。
チェインを作成した時と同じ手順で末尾の「平文」を導き出したら、記録してあるチェインの末尾の「平文」と比較し、一致しているものがないかを調べます。
一致している場合は、一致したチェインの先頭が不正入手した「ハッシュ値」の元のデータ(平文)なので処理は終了です。
一致していない場合は、更に前へ還元関数を使用して同様の手順を行います。このように記録したチェーンの末尾に一致する平文が得られるまで、開始列までさかのぼる形で処理を繰り返していきます。