ベン図とは

ベン図

ベン図とは、集合と集合の関係を視覚的に示す図のことです。ベン図は集合の関係性を表すもので、集合演算や論理演算を視覚的にわかりやすく表現する手法として用いられています。

集合演算には次のようなものがあります。

スポンサーリンク

積集合（AかつB）

積集合とは、2つの集合に対して両方に入っているものを集めた集合のことです。

例えば、Aという集合と、Bという集合がある場合、AとB両方にあてはまるものを集めた集合のことで、ベン図で表すと次の通りです。赤くなっている部分が積集合。

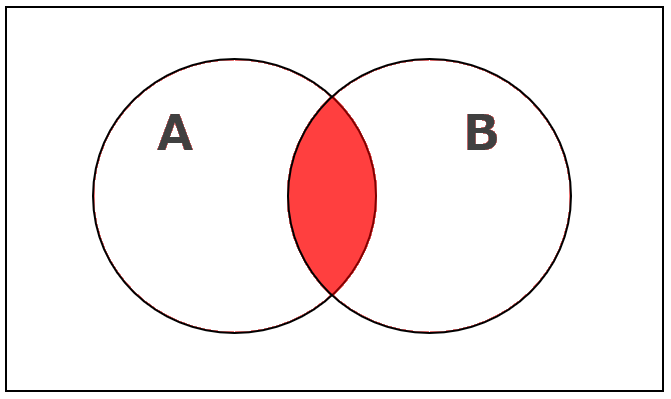
もう少し具体的な例で例えると、野球チームに入っているのがA、サッカーチームに入っているのがBとすると、野球チーム（A）とサッカーチーム（B）の両方に入っている人達が積集合です。

「AかつB」の範囲が該当し、演算記号では（A∩B）という記号であらわします。

和集合（AまたはB）

和集合とは、2つの集合に対してどちらかに入っている(両方も含む)ものを集めた集合のことです。

例えば、Aという集合と、Bという集合がある場合、AとBのどちらかにあてはまるものを集めた集合のことで、ベン図で表すと次の通りです。赤くなっている部分が和集合。

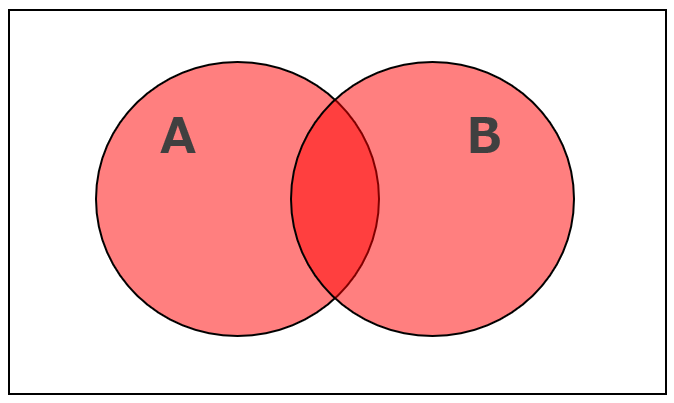
もう少し具体的な例で例えると、野球チームに入っているのがA、サッカーチームに入っているのがBとすると、野球チーム（A）または サッカーチーム（B）に入っている人達が和集合です。

「AまたはB」の範囲が該当し、演算記号では（A∪B）という記号であらわします。

補集合（Aではない）

補集合とは、否定をあらわす集合のことです。

例えば、Aという集合がある場合、Aに含まれないものを集めた集合のことで、ベン図で表すと次の通りです。赤くなっている部分が補集合。

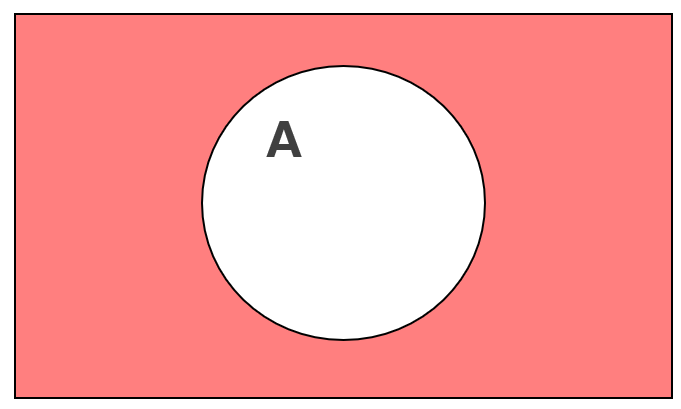
もう少し具体的な例で例えると、野球チームに入っているのがAとすると、野球チーム（A）に入っていない人達が補集合です。

「Aではない」という範囲に該当し、演算記号ではという記号であらわします。

差集合（AだがBではない）

差集合とは、ある集合の中から別の集合に属する要素を取り去って得られる集合のことです。

例えば、Aという集合と、Bという集合がある場合、Aの中でBにあてはまるものを取り除いた集合のことで、ベン図で表すと次の通りです。赤くなっている部分が差集合。

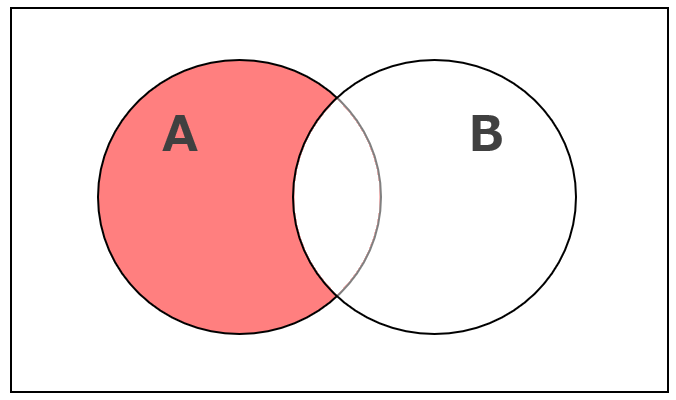
もう少し具体的な例で例えると、野球チームに入っているのがA、サッカーチームに入っているのがBとすると、野球チーム（A）にしか入っていない人達が差集合です。

「AだがBではない」という範囲が該当し、演算記号では（A-B）という記号であらわします。

対称差集合（AまたはBだがAB両方ではない）

対称差集合とは、2つの集合に対してどちらかに入っているものを集めた集合から、両方入っているものを取り除いた集合のことです。

例えば、Aという集合と、Bという集合がある場合、AとBのどちらかにあてはまるものを集めた集合から両方入っているものを取り除いた集合のことで、ベン図で表すと次の通りです。赤くなっている部分が対称差集合。

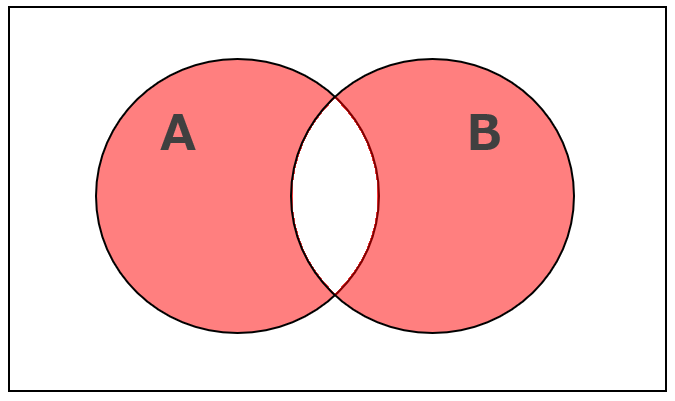
もう少し具体的な例で例えると、野球チームに入っているのがA、サッカーチームに入っているのがBとすると、野球チーム（A）のみ、または サッカーチーム（B）のみに入っている人達が対称差集合です。

「AまたはBだが、AB両方ではない」という範囲が該当し、演算記号では（A△B）という記号であらわします。