

問題
数値を2進数で表すレジスタがある。このレジスタに格納されている正の整数xを10倍する操作はどれか。ここで,桁あふれは,起こらないものとする。
- ア:xを2ビット左にシフトした値にxを加算し,更に1ビット左にシフトする。
- イ:xを2ビット左にシフトした値にxを加算し,更に2ビット左にシフトする。
- ウ:xを3ビット左にシフトした値と,xを2ビット左にシフトした値を加算する。
- エ:xを3ビット左にシフトした値にxを加算し,更に1ビット左にシフトする。
基本情報技術者平成29年秋期 午前問1
問題
32ビットのレジスタに16進数ABCDが入っているとき,2ビットだけ右に論理シフトしたときの値はどれか。
ア:2AF3 イ:6AF3 ウ:AF34 エ:EAF3
基本情報技術者平成25年秋期 午前問2
基本情報技術者試験の過去問だけを見ると難しく感じるシフト演算の問題。ただ、シフト演算の動きを理解してしまえば簡単に解くことができます。
本記事では「シフト演算」について図解で分かりやすく解説していきます。
本記事で学べること
- シフト演算の論理シフトと算術シフトを理解
- 基本情報技術者試験の過去問の解き方を学ぶ
目次
シフト演算とは
シフト演算とは、2進数をあらわすビット列を左または右にずらす操作のことです。
例えば、10進数で考えると「770」という数字を10倍すると「7700」、1/10倍すると「77」となり、10倍は1桁増やす操作(左にシフトする)であり、1/10倍は1桁減らす操作(右にシフトする)です。
この操作は2進数でも同じであり、「100」(10進数:4)という2進数を2倍すると「1000」(10進数:8)になり、1/2倍すると「10」(10進数:2)になります。
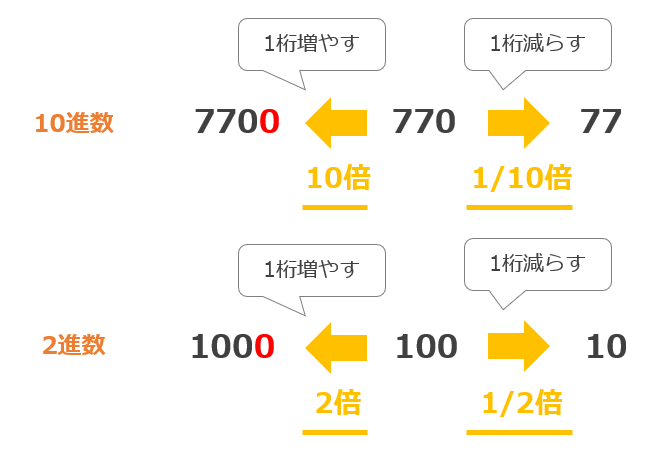
このように、ビット列を左にずらす(左にシフト)と元の値の2倍、右にずらす(右にシフト)と元の値の1/2倍という計算結果を簡単に得ることができます。コンピュータはこのシフト演算を使い、掛け算や割り算をおこなっています。

論理シフト
論理シフトとは、符号を考慮しないシフト演算のことです。
スポンサーリンク
左論理シフト
ビット列全体を左にずらす論理シフトのことを「左論理シフト」といいます。
以下は左論理シフトのイメージ例です。※8ビットの例
2進数「00001100」(10進数:12)を左に2ビットシフトすると元の数を22倍(12 × 2 × 2 = 48)にした値を得ることができます。
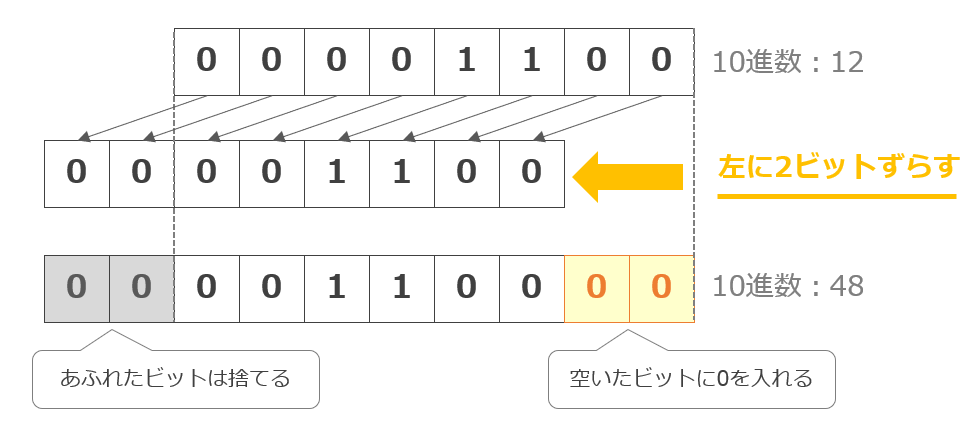
左論理シフトでは、あふれたビットを捨てます。ただし「0」ではなく「1」があふれた場合は、オーバーフローとなり、ビット列であらわせる数の限界を超えてしまうという現象が発生します。
右論理シフト
ビット列全体を右にずらす論理シフトのことを「右論理シフト」といいます。
以下は右論理シフトの例です。※8ビットの例
2進数「00001100」(10進数:12)を右に2ビットシフトすると元の数を1/22倍(12 × 1/2 × 1/2 = 3)にした値を得ることができます。
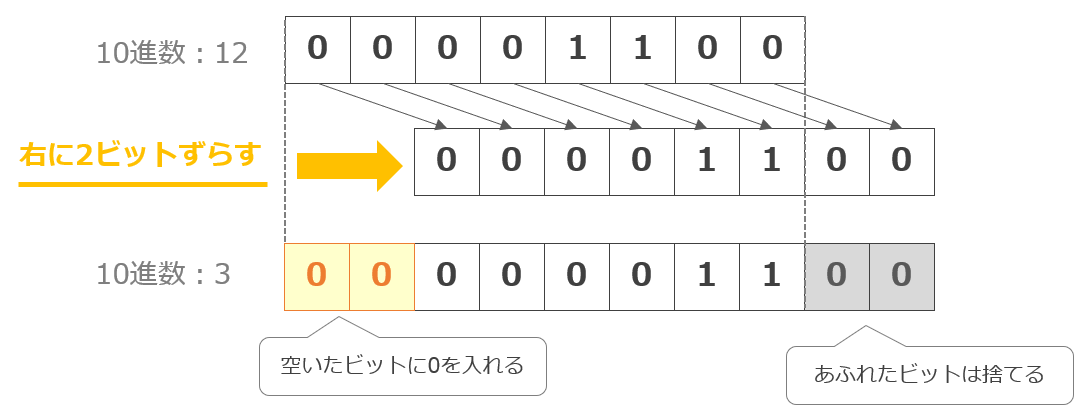
算術シフト
算術シフトとは、符号を考慮するシフト演算のことです。算術シフトでは、先頭の1ビットを符号ビット(正 = 0、負 = 1)として扱います。
左算術シフト
ビット列全体を左にずらす算術シフトのことを「左算術シフト」といいます。
以下は左算術シフトのイメージ例です。※8ビットの例
先頭の符号ビットは固定なので、シフト操作は残りの7ビットに対して行われます。2進数「11100100」(10進数:-28)を左に2ビットシフトすると元の数を22倍(-28 × 2 × 2 = -112)にした値を得ることができます。
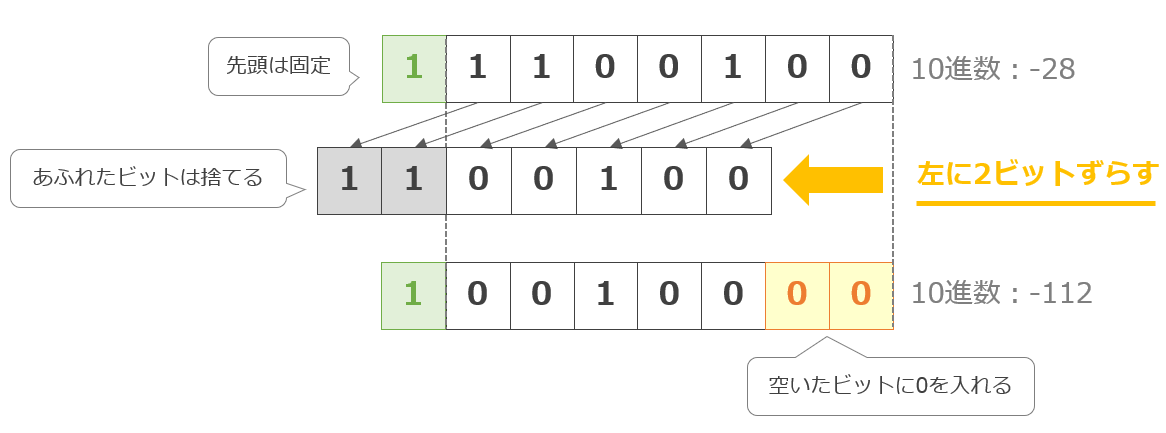
左算術シフトでは、あふれたビットを捨てます。ただし符号ビットと異なる値があふれた場合は、オーバーフローとなり、ビット列であらわせる数の限界を超えてしまうという現象が発生します。
スポンサーリンク
右算術シフト
ビット列全体を右にずらす算術シフトのことを「右算術シフト」といいます。
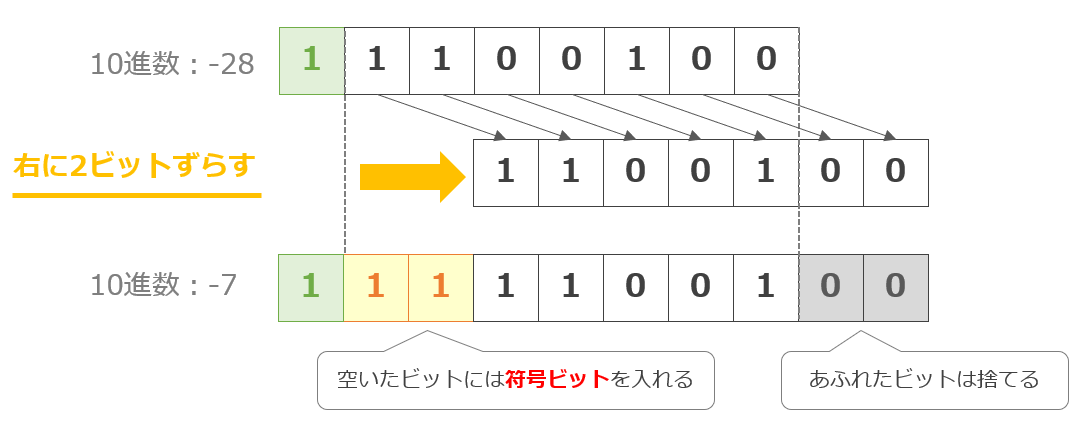
以下は右算術シフトのイメージ例です。※8ビットの例
先頭の符号ビットは固定なので、シフト操作は残りの7ビットに対して行われます。(右算術シフトでは空いたビットには0ではなく符号ビットが入る)
2進数「11100100」(10進数:-28)を右に2ビットシフトすると元の数を1/22倍(-28 × 1/2 × 1/2 = -7)にした値を得ることができます。
基本情報技術者試験 過去問の解説
基本情報技術者平成29年秋期 午前問1
問題
数値を2進数で表すレジスタがある。このレジスタに格納されている正の整数xを10倍する操作はどれか。ここで,桁あふれは,起こらないものとする。
- ア:xを2ビット左にシフトした値にxを加算し,更に1ビット左にシフトする。
- イ:xを2ビット左にシフトした値にxを加算し,更に2ビット左にシフトする。
- ウ:xを3ビット左にシフトした値と,xを2ビット左にシフトした値を加算する。
- エ:xを3ビット左にシフトした値にxを加算し,更に1ビット左にシフトする。
この問題はア~エの文章を式に変えて計算することで、答えを求めることができます。
ポイント
nビット左シフトは2n倍
nビット右シフトは1/2n倍
アを求める
- xを2ビット左にシフト:「x × 22 = x × 4 = 4x」・・・①
- ①にxを加算:「4x + x = 5x」・・・②
- ②を更に1ビット左にシフト:「5x × 21 = 5x × 2 = 10x」
イを求める
- xを2ビット左にシフト:「x × 22 = x × 4 = 4x」・・・①
- ①にxを加算:「4x + x = 5x」・・・②
- ②を更に2ビット左にシフト:「5x × 22 = 5x × 4 = 20x」
ウを求める
- xを3ビット左にシフト:「x × 23 = x × 8 = 8x」・・・①
- xを2ビット左にシフト:「x × 22 = x × 4 = 4x」・・・②
- ①と②を加算:「8x + 4x = 12x」
エを求める
- xを3ビット左にシフト:「x × 23 = x × 8 = 8x」・・・①
- ①にxを加算:「8x + x = 9x」・・・②
- ②を更に1ビット左にシフト:「9x × 21 = 9x × 2 = 18x」

基本情報技術者平成25年秋期 午前問2
問題
32ビットのレジスタに16進数ABCDが入っているとき,2ビットだけ右に論理シフトしたときの値はどれか。
ア:2AF3 イ:6AF3 ウ:AF34 エ:EAF3
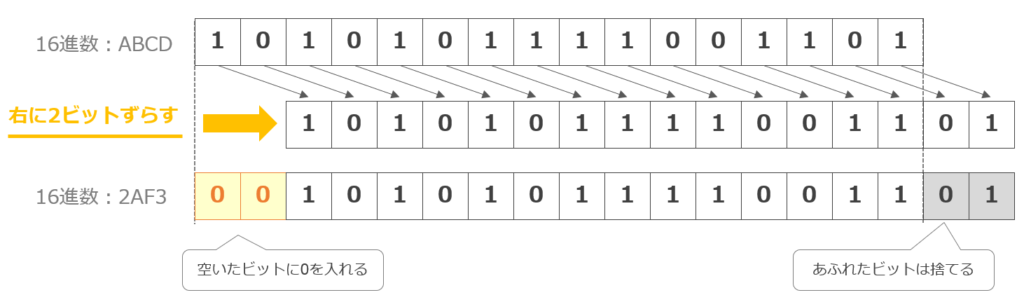
この問題は、16進数「ABCD」を2進数に変換し、2ビット右論理シフトを実施して得られた結果を16進数に戻すことで求めることができます。
求め方
[16進数ABCDを2進数に変換する]
1010 1011 1100 1101・・・①
(16進数→2進数の変換:A→1010、B→1011、C→1100 、D→1101)
[①を2ビット右に論理シフトする]
0010 1010 1111 0011 01・・・②
[②を16進数に戻す]
2AF3
(2進数→16進数の変換:0010→2、1010→A、1111→F、0011→3)

基本情報技術者試験おすすめの参考書・問題集
| いちばんやさしい 基本情報技術者 | 『基本情報技術者試験』試験に、短期間で一発合格するための試験対策本。ITの知識がまったくない、未経験者やでもスラスラと学習を進められるよう、丁寧に解説。 |
| かやのき先生の基本情報技術者教室 | 基本情報技術者をめざす方のためのやさしいオールインワンタイプの参考書&問題集。イラストや豊富な図解・例え話を駆使して理解しやすく・記憶に残りやすいように説明。 |
| 基本情報技術者 パーフェクトラーニング過去問題集 | 科目A・Bともに万全の対策ができる、定番の過去問題集!科目A・科目Bの両方について万全の対策ができる。 |
| キタミ式イラストIT塾 基本情報技術者 | すべての解説をイラストベースで行っているため,とてもわかりやすい解説本。いちばん最初に読む基本情報技術者試験関連の書籍を探している人におすすめ! |
| 出るとこだけ!基本情報技術者[科目B] | 基本情報技術者【科目B】対策の定番書!前提知識+解き方+試験問題を掲載。効率よく学習できる。 |
| 基本情報技術者 合格教本 | 出題範囲を体系的にきちんと理解しながら学習したい人におすすめ!基本情報技術者試験の定番テキストの改訂版。 |
| 基本情報技術者 超効率の教科書+よく出る問題集 | 動画でスムーズに学習スタート、テキストでしっかり理解度を深める!よく出る問題を反復学習することで、合格に直結するチカラが身に付く! |

