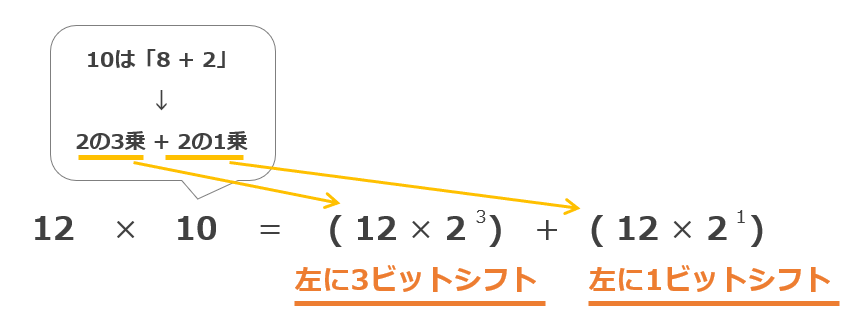シフト演算とは
シフト演算とは、2進数をあらわすビット列を左または右にずらす操作のことです。
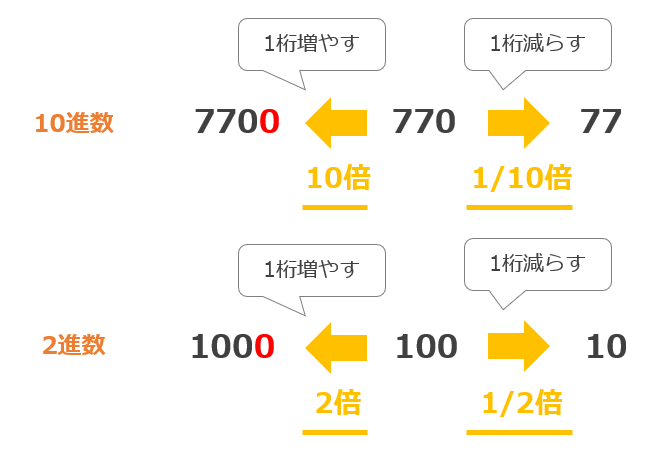
例えば、10進数で考えると「770」という数字を10倍すると「7700」、1/10倍すると「77」となり、10倍は1桁増やす操作であり、1/10倍は1桁減らす操作です。
スポンサーリンク
この操作は2進数でも同じであり、「100」(10進数:4)という2進数を2倍すると「1000」(10進数:8)になり、1/2倍すると「10」(10進数:2)です。
このように、ビット列を左にずらすと元の値の2倍、右にずらすと元の値の1/2倍という計算結果を簡単に得ることができます。コンピュータはこのシフト演算を使い、掛け算や割り算を行っています。
論理シフト
論理シフトとは、符号を考慮せずに行うシフト演算のことです。
左論理シフト
ビット列全体を左にずらす論理シフトのことを「左論理シフト」といいます。
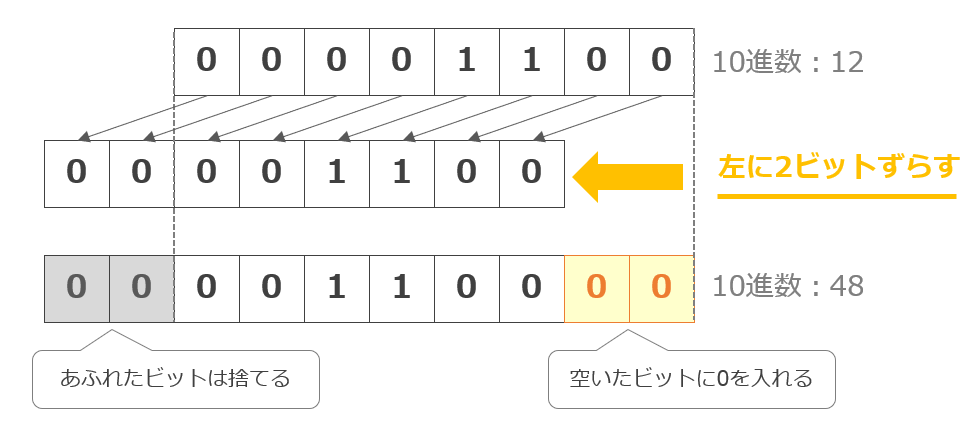
左論理シフトのイメージ例は以下の通り。※8ビットの例
左にずらしたビット数をnとすると、左論理シフト後は元の数を2のn乗倍したものであり、上記の例では、左に2ビットずらしているので、左論理シフト後の値は「12 × 2 × 2 = 48」と元の数を2の2乗倍にした値となっています。
左論理シフトでは、あふれたビットは捨てます。ただし「0」ではなく「1」があふれた場合は、オーバーフローとなり、ビット列であらわせる数の限界を超えてしまうという現象が起きます。
右論理シフト
ビット列全体を右にずらす論理シフトのことを「右論理シフト」といいます。
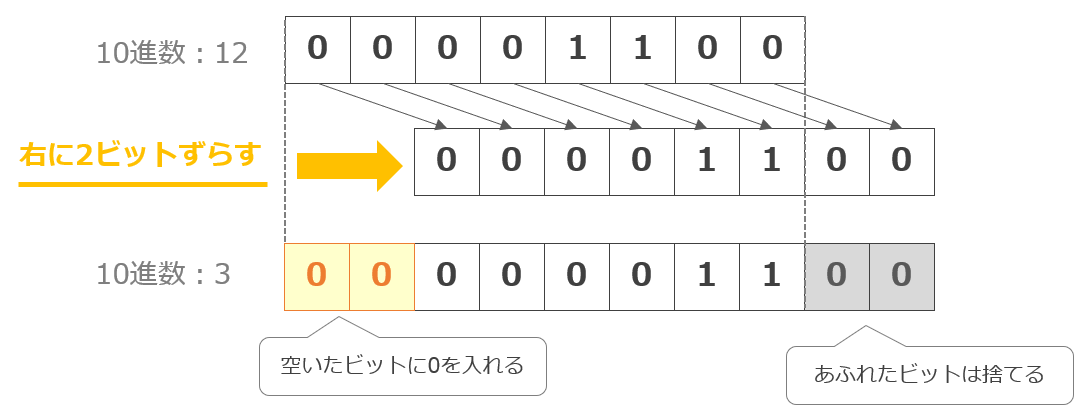
右論理シフトのイメージ例は以下の通り。※8ビットの例
右にずらしたビット数をnとすると、右論理シフト後は元の数を1/2のn乗倍したものであり、上記の例では、右に2ビットずらしているので、右論理シフト後の値は「12 ÷ 2 ÷ 2 = 3」と元の数を1/2の2乗倍にした値となっています。
右論理シフトでは、あふれたビットが「0」ではなく「1」の場合は、割り算した結果の余りとなります。
算術シフト
算術シフトとは、符号を考慮して行うシフト演算のことです。算術シフトでは、先頭の1ビットを符号ビット(正 = 0、負 = 1)として扱うのが特徴です。
左算術シフト
ビット列全体を左にずらす算術シフトのことを「左算術シフト」といいます。
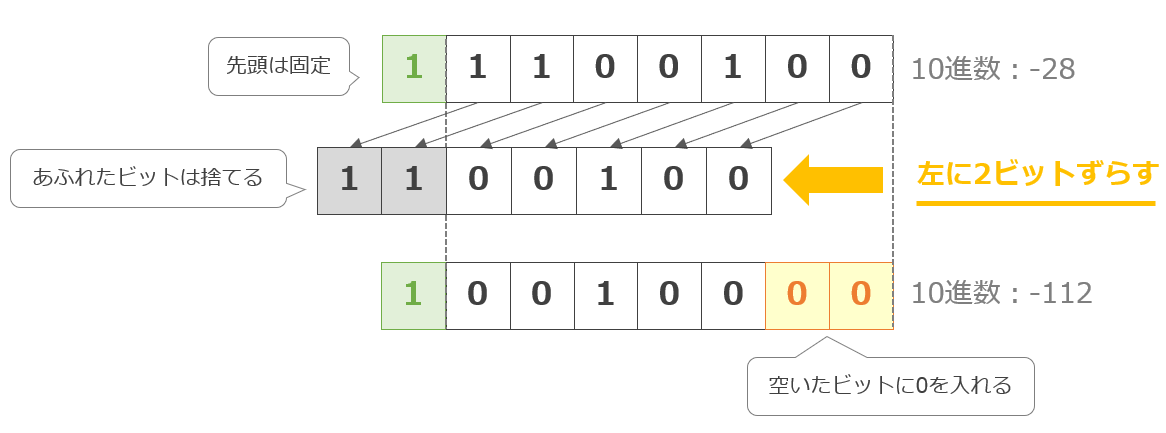
左算術シフトのイメージ例は以下の通り。※8ビットの例
先頭は符号ビットで固定なので、シフト操作は残りの7ビットに対して行われます。左にずらすと2のn乗倍になるのは、左論理シフトと同じです。
上記の例では、符号ビットが「1」(マイナスの値)である値(10進数で-28)を左に2ビットずらしています。その結果「-28 × 2 × 2 = -112」と元の数を2の2乗倍にした値となっています。
左算術シフトでは、あふれたビットは捨てます。ただし符号ビットと異なる値があふれた場合は、オーバーフローとなり、ビット列であらわせる数の限界を超えてしまうという現象が起きます。
右算術シフト
ビット列全体を右にずらす算術シフトのことを「右算術シフト」といいます。
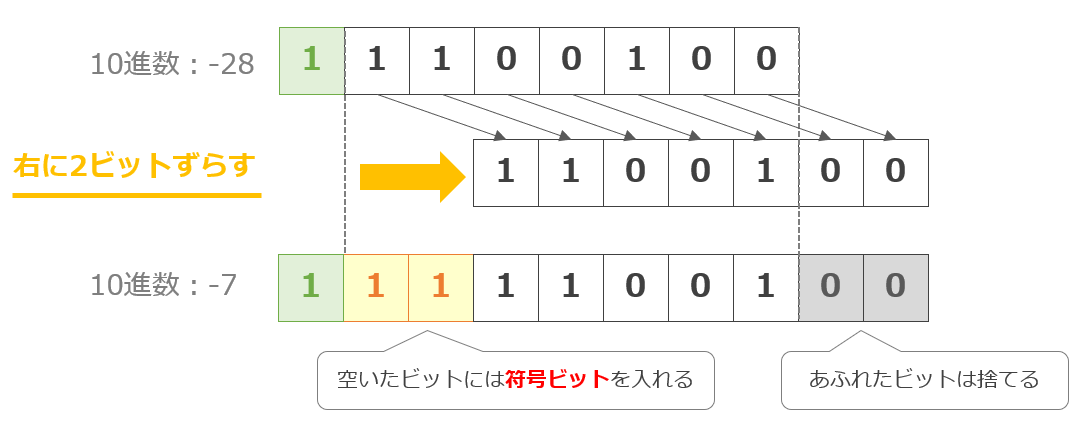
右算術シフトのイメージ例は以下の通り。※8ビットの例
先頭は符号ビットで固定なので、シフト操作は残りの7ビットに対して行われます。右にずらすと1/2のn乗倍になるのは、左論理シフトと同じです。
ただし、右算術シフトでは空いたビットには符号ビットが入ります。
上記の例では、符号ビットが「1」(マイナスの値)である値(10進数で-28)を右に2ビットずらしています。その結果「-28 ÷ 2 ÷ 2 = -7」と元の数を1/2の2乗倍にした値となっています。
右算術シフトでは、右論理シフト同様 あふれたビットが「0」ではなく「1」の場合は、割り算した結果の余りとなります。
シフト演算を用いた掛け算と割り算
スポンサーリンク
シフト演算による掛け算
シフト演算による掛け算は、次のように2のn乗同士の足し算に置き換えて計算を行います。
例えば、10進数の「12×10」という掛け算は、10は「8+2」なので「2の3乗 + 2の1乗」に置き換えて計算します。
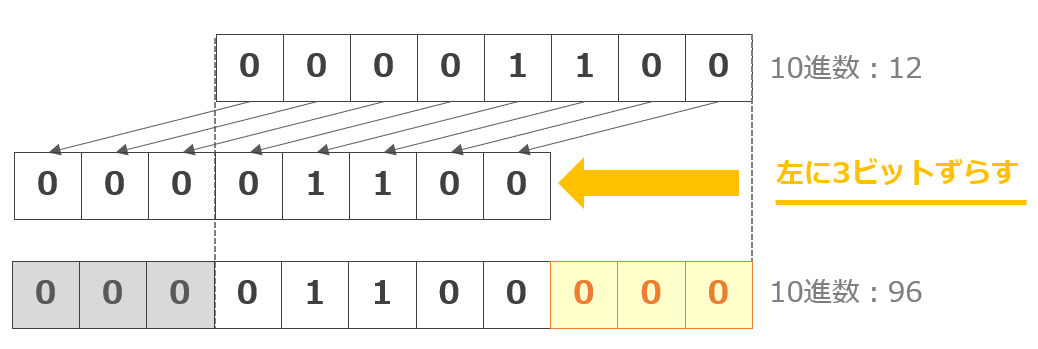
まず、12×2の3乗は「00001100」(10進数:12)を左に3ビットずらします。その結果は「01100000」(10進数:96)です。
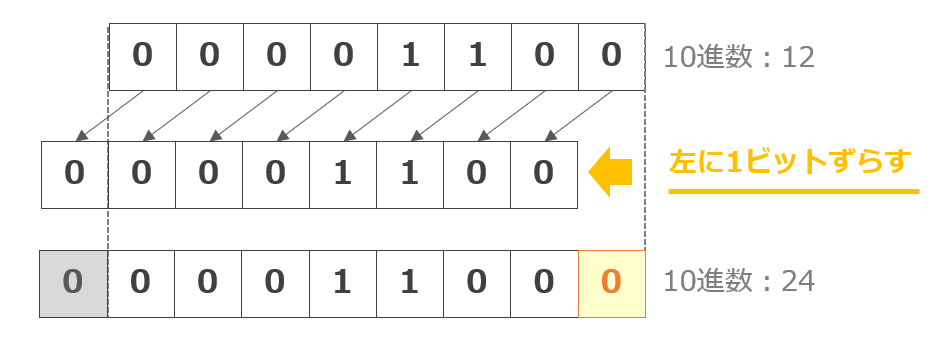
次に、12×2の1乗は「00001100」(10進数:12)を左に1ビットずらします。その結果は「0001100」(10進数:24)です。
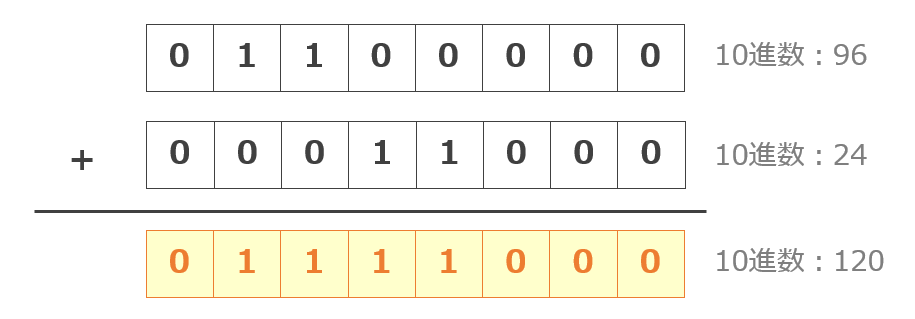
最後に「01100000」(10進数:96)と「0001100」(10進数:24)を加算すればシフト演算による掛け算は終了です。

シフト演算による割り算
シフト演算による割り算は、割られる数から割る数を何回引けるかを考えます。

例えば「15 ÷ 5」をシフト演算で計算してみます。
シフト演算による割り算は、割られる数から割る数を何回引けるかを考えます。
単純に引き算すると以下であり、割られる数「15」は割る数「5」で3回引けるので、答えは3であるのがわかります。
15 - 5 = 10
10 - 5 = 5
5 - 5 = 0
これをシフト演算で考えると

まず、10進数の「15÷5」を2進数に変換すると「1111÷101」です。そして、割られる数「1111」から割る数「101」が何回引けるか計算すると
1111 - 1010 = 101 ← 左に1ビットシフト (※左シフトで桁を合わせる)
101 - 101 = 0 ← 左に0ビットシフト
となり、その結果(左シフトした値)を加算「21 + 20」することで、「2+1=3」と答えを求めることができます。