オートマトン
オートマトン(英:automaton)とは、自動人形という意味を持つ言葉であり、コンピュータの状態、遷移をモデル化したものです。
例えば、自動販売機は「お金を入れる」(入力)→「ボタンが点灯」(状態の遷移)、「点灯したボタンを押す」(入力)→「ジュースが出てくる」(状態の遷移)のような動作をします。
このように状態の遷移にともなう動作をモデル化してあらわすのがオートマトンです。
オートマトンにはいくつかの種類があり、その中でも代表的なモデルが「有限オートマトン」です。


スポンサーリンク
有限オートマトン
有限オートマトン(英:finite automaton)とは、状態や遷移の数が有限個であらわされるオートマトンのことです。
有限オートマトンは次のような「状態遷移表」と「状態遷移図」を用いて表現します。
■状態遷移表の例
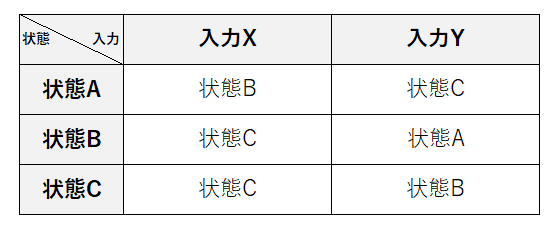
■状態遷移図の例
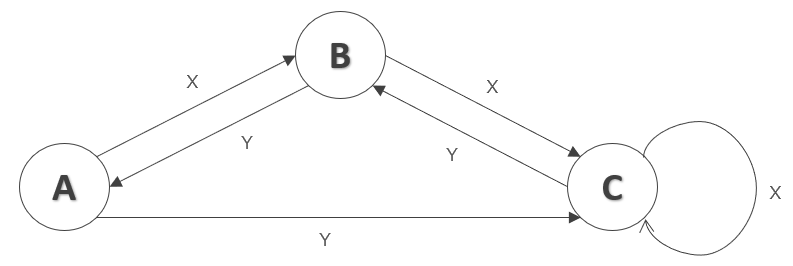
状態遷移図は、次の記号で表現します。
| 名称 | 記号 | 説明 |
| 状態 | 状態をあらわす | |
| 受理状態 | 受理状態をあらわす | |
| 遷移 | 遷移をあらわす |
有限オートマトンには「受理」と「非受理」があり、入力終了時に受理状態であれば受け付けを完了し、受理状態でないものは非受理となり受け付けません。
有限オートマトンの実行例

例えば、次のような状態遷移表があるとします。
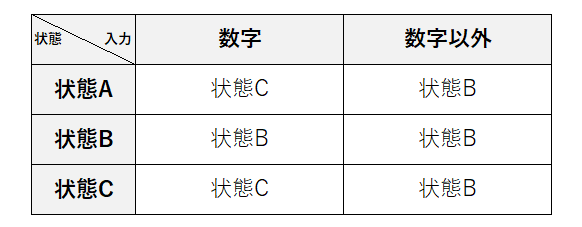
この状態遷移表から、状態遷移図を作ると次のような図が作成できます。この状態遷移図は入力データが「すべて数値なら受理」、「数値以外があれば非受理」という有限オートマトンです。※状態Aを初期状態(開始地点)としています。
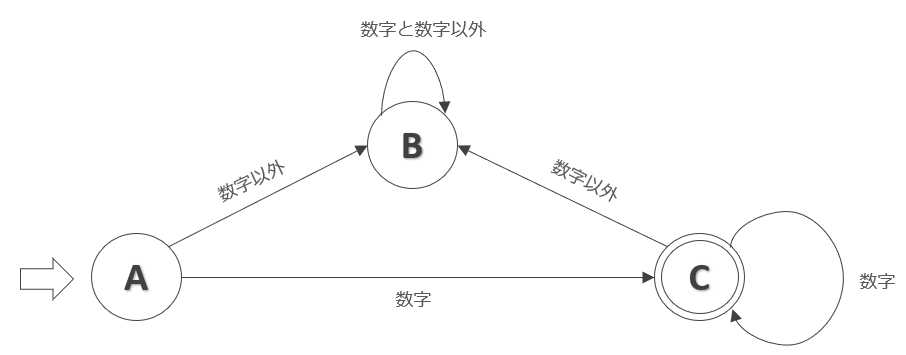
受理の例(入力データ「12」)
この状態遷移図に入力データ「12」を与えたときの流れは次の通りです。
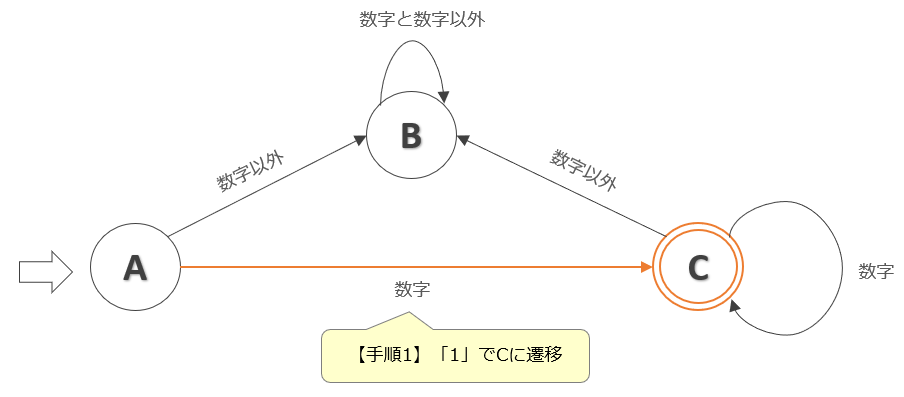
【手順1】「1」で「状態C」に遷移
初期状態は「状態A」なので「状態A」を開始地点とします。はじめの入力データ「1」は数値なので「状態A」→「状態C」に遷移します。
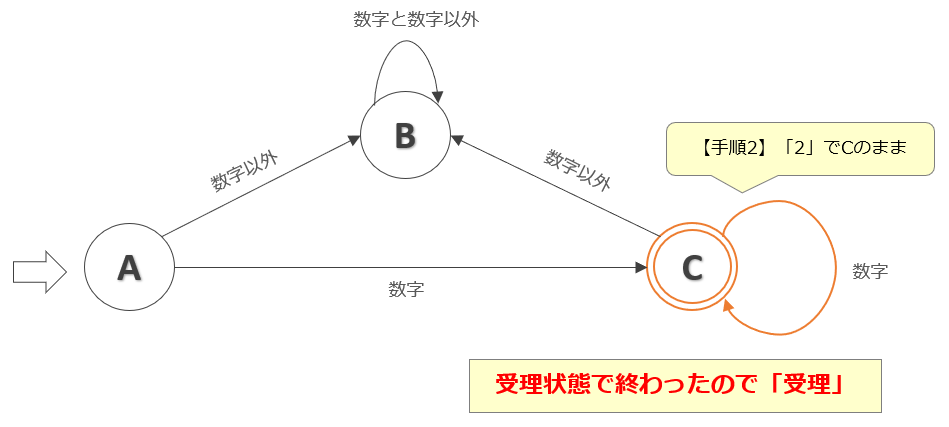
[手順2]「2」で「状態C」のままとなり"受理"
続いての入力データ「2」は数値なので「状態C」のままです。これで入力は終了です。
入力終了時の状態が「受理状態」なので、入力「12」は受理します。
非受理の例(入力データ「1a」)
この状態遷移図に入力データ「1a」を与えたときの流れは次の通りです。
【手順1】「1」で「状態C」に遷移
初期状態は「状態A」なので「状態A」を開始地点とします。はじめの入力データ「1」は数値なので「状態A」→「状態C」に遷移します。

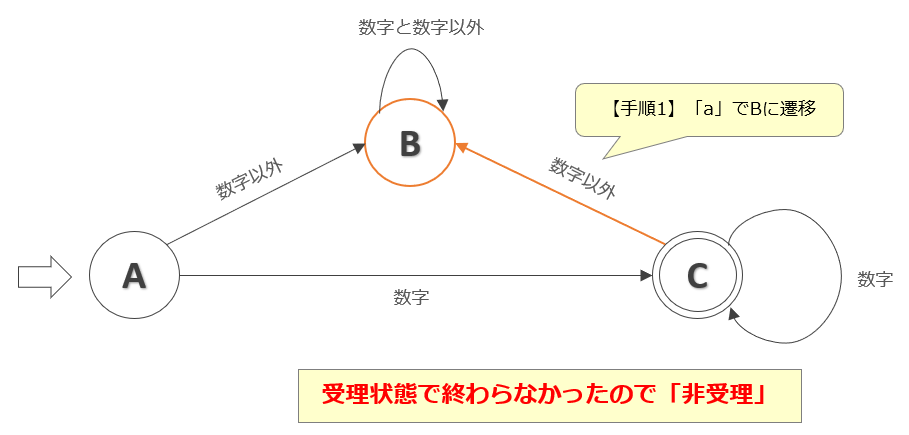
[手順2]「a」で「状態B」となり"非受理"
続いての入力データ「a」は数値ではないので「状態C」→「状態B」に遷移します。これで入力は終了です。
入力終了時の状態が「受理状態」ではないので、入力「1a」は非受理となり、受理しません。