

問題
出現頻度の異なるA,B,C,D,Eの5文字で構成される通信データを,ハフマン符号化を使って圧縮するために,符号表を作成した。aに入る符号として,適切なものはどれか。
| 文字 | 出現確率(%) | 符号 |
| A | 26 | 00 |
| B | 25 | 01 |
| C | 24 | 10 |
| D | 13 | a |
| E | 12 | 111 |
ア:001 イ:010 ウ:101 エ:110
基本情報技術者平成30年秋期 午前問4
問題
表は,文字A~Eを符号化したときのビット表記と,それぞれの文字の出現確率を表したものである。1文字当たりの平均ビット数は幾らになるか。
| 文字 | ビット表記 | 出現確率(%) |
| A | 0 | 50 |
| B | 10 | 30 |
| C | 110 | 10 |
| D | 1110 | 5 |
| E | 1111 | 5 |
ア:1.6 イ:1.8 ウ:2.5 エ:2.8
基本情報技術者平成23年特別 午前問3
基本情報技術者試験や応用情報技術者試験で出題される問題である ハフマン符号化、過去問だけをみると難しく感じる問題です。
ただ、ハフマン符号化の動きを理解してしまえば、そこまで難しい問題ではありません。
本記事では、ハフマン符号化について図解で分かりやすく解説しています。
本記事で学べること
- ハフマン符号化について理解する
- ハフマン木の作り方を覚える
- 基本情報技術者試験の過去問の解き方を学ぶ
目次
符号化とは
符号化とは、データを"0"と"1"の2進数に置き換えることです。
コンピュータは"0"と"1"の集まりしか理解できません。そのため、コンピュータに処理をさせるにはデータを2進数に変換する必要があります。この作業が符号化です。
スポンサーリンク
例えば「A」を「00」、「B」を「01」、「C」を「10」、「D」を「11」というように置き換えるものとします。
この場合、文字列「ABCD」は「000101」に置き換えることができます。この作業が符号化です。

符号化は、処理効率の側面からできるだけ少ないビット数で2進数へ変換することが求められています。
例えば「AAA」を「000000」の6ビットに変換するよりも「000」の3ビットに変換できた方が、データ量が少なくなり、メモリの使用量が減り処理の高速化に繋がります。
このデータをできるだけ少ないビット数で2進数へ変換する方法の1つが「ハフマン符号化」です。
ハフマン符号化とは
ハフマン符号化とは、データの出現頻度に着目した圧縮方法です。出現確率が高いデータには短い符号を、低いデータには長い符号を与えることで圧縮を効率よく行う方法です。
例えば「ABAAACBDBA」という文字列を以下のルールで符号化すると「00010000001001110100」となり、長さは20ビットです。
- A → 00
- B → 01
- C → 10
- D → 11
この「ABAAACBDBA」をハフマン符号化で符号化すると「01000011010111100」となり、長さは17ビットです。(85%の圧縮率 ※圧縮率は文字の出現頻度により変わる)
- A → 0 (出現頻度:5回)
- B → 10 (出現頻度:3回)
- C → 110 (出現頻度:1回)
- D → 111 (出現頻度:1回)
このようにハフマン符号化を使うことで、データをできるだけ少ないビット数で2進数へ変換することができます。
ハフマン符号化でデータを圧縮するまでの流れ
ハフマン符号化では、ハフマン木と呼ばれる木構造を用いて符号化します。今回の例では「ABAAACBDBA」のデータをハフマン符号化で符号化します。
スポンサーリンク
ハフマン木(木構造)の作り方
ハフマン木は次の3つの手順で作成します。
ハフマン木の作成手順
- 各データを出現確率の高い順に並べる
- 最も出現確率の低い2つを1つにする
- 手順2を繰り返して木構造を完成させる
【手順1】各データを出現確率の高い順に並べる
各データを出現確率の高い順に並べます。
今回の例では「ABAAACBDBA」のデータをハフマン符号化で符号化します。出現確率はAが50%(5回)、Bが30%(3回)、CとDが10%(1回)なので、出現確率の高い順(A、B、C、D)に並べます。

【手順2】最も出現確率の低い2つを1つにする
出現確率の高い順に並べた後は、最も出現確率の低い2つをつなぐ「親」を作り1つにします。今回の例では「C」と「D」が最も出現確率が低いので、2つを繋ぐ「親CD」を作ります。
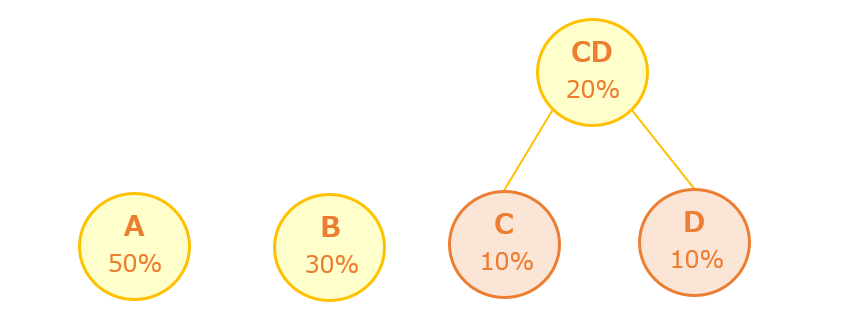
【手順3】手順2を繰り返して木構造を完成させる
次に最も出現確率が低い2つは「B」と「CD」なので、「B」と「CD」をつなぐ「親BCD」を作ります。
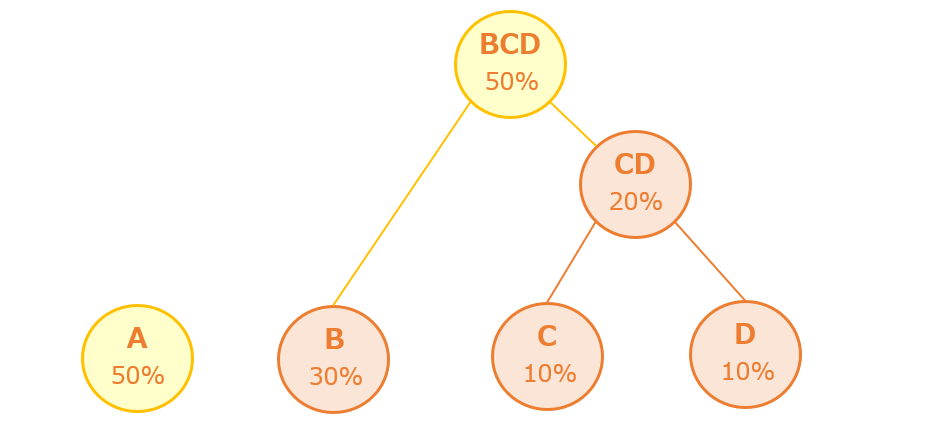
最後に「A」と「BCD」をつないで木構造(ハフマン木)の完成です。
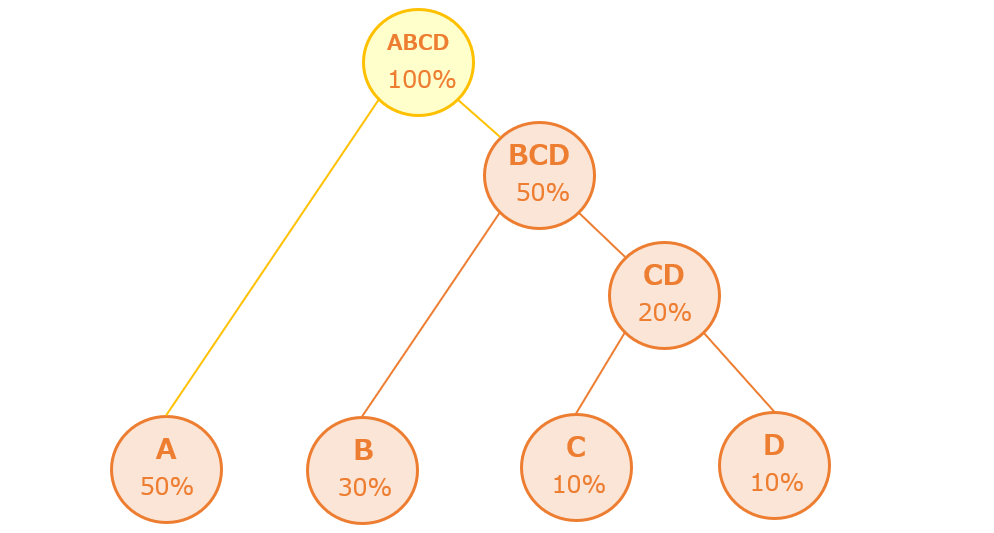
ハフマン木(木構造)に「0」と「1」を割り振る
作成したハフマン木(木構造)に「0」と「1」を割り振ります。今回の例では左に「0」、右に「1」を割り振っています。(左に「1」、右に「0」でも可)
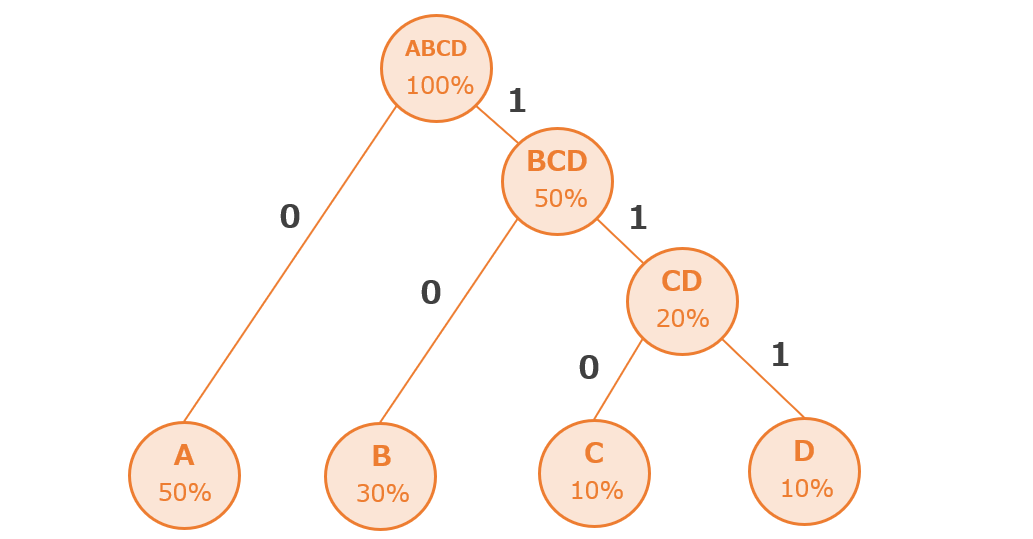
ハフマン木(木構造)から符号表を作る
ハフマン木(木構造)を上から順にたどり符号表(文字と符号の対応表)を作ります。
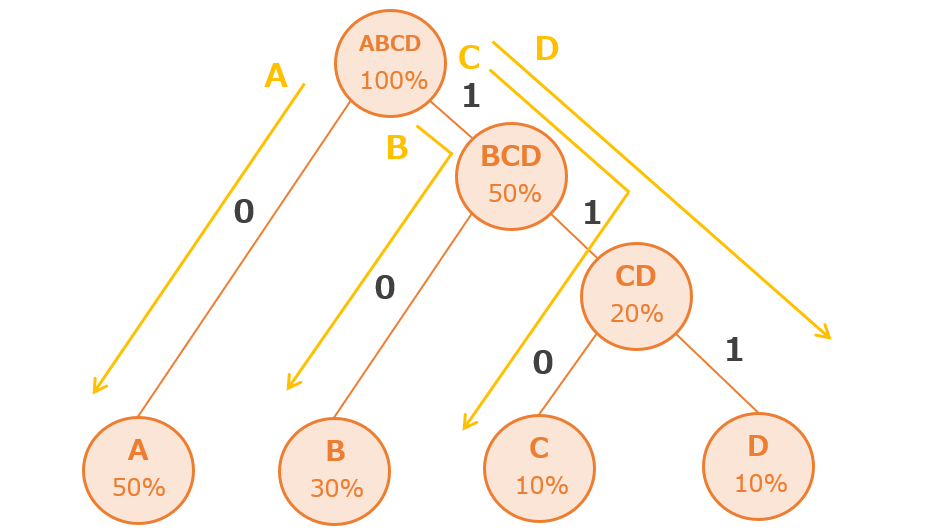
- Aは「ABCD」→「A」なので「0」
- Bは「ABCD」→「BCD」→「B」なので「10」
- Cは「ABCD」→「BCD」→「CD」→「C」なので「110」
- Dは「ABCD」→「BCD」→「CD」→「D」なので「111」
[符号表]
| 文字 | 出現確率(%) | 符号 |
| A | 50 | 0 |
| B | 30 | 10 |
| C | 10 | 110 |
| D | 10 | 111 |
この符号表どおりに符号化すると「ABAAACBDBA」を「01000011010111100」に変換できます。
平均ビット長の求め方
各文字を表すビット数とその出現確率をかけたものを足し合わせて平均ビット数を求めることができます。
例えば、上記の符号表の平均ビット長は1.7ビットです。
平均ビット長の計算
①. 各文字を表すビット数とその出現確率をかける
- A:1ビット × 0.5 = 0.5ビット ※符号(1)は1ビット 確率は50%
- B:2ビット × 0.3 = 0.6ビット ※符号(10)は2ビット 確率は30%
- C:3ビット × 0.1 = 0.3ビット ※符号(110)は3ビット 確率は10%
- D:3ビット × 0.1 = 0.3ビット ※符号(110)は3ビット 確率は10%
②. ①を合算する
0.5 + 0.6 + 0.3 + 0.3 = 1.7
基本情報技術者試験 過去問の解説
スポンサーリンク
基本情報技術者平成30年秋期 午前問4
問題
出現頻度の異なるA,B,C,D,Eの5文字で構成される通信データを,ハフマン符号化を使って圧縮するために,符号表を作成した。aに入る符号として,適切なものはどれか。
| 文字 | 出現確率(%) | 符号 |
| A | 26 | 00 |
| B | 25 | 01 |
| C | 24 | 10 |
| D | 13 | a |
| E | 12 | 111 |
ア:001 イ:010 ウ:101 エ:110
ハフマン符号化は出現率の高い文字は短い符号に変換し、出現率の低い文字は長い符号に変換します。
この際に符号は重複しないようする必要があります。(設問の表を見ると"00"、"01"、"10"、"111"は既に割当て済なので、Dにはこれ以外のビット列から開始する必要がある)
- アの"00"からはじまり「A」と重複するので不正解
- イは"01"からはじまり「B」と重複するので不正解
- ウは"10"からはじまり「C」と重複するので不正解
- エは"110"と「A」「B」「C」「E」のいずれにも重複していないので正解
また下記のように、符号表からハフマン木を作成して考えることもできます。ハフマン木を作成した結果、Dの符号が「110」になることがわかります。
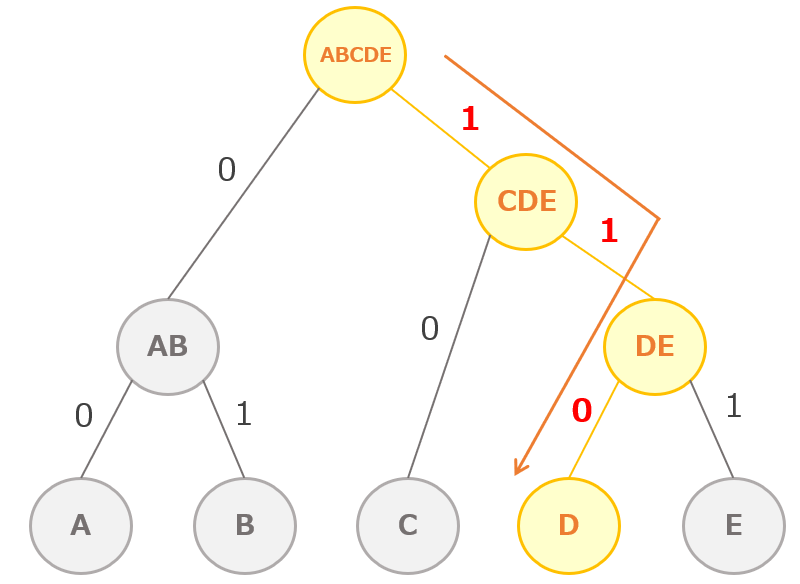
基本情報技術者平成23年特別 午前問3
問題
表は,文字A~Eを符号化したときのビット表記と,それぞれの文字の出現確率を表したものである。1文字当たりの平均ビット数は幾らになるか。
| 文字 | ビット表記 | 出現確率(%) |
| A | 0 | 50 |
| B | 10 | 30 |
| C | 110 | 10 |
| D | 1110 | 5 |
| E | 1111 | 5 |
ア:1.6 イ:1.8 ウ:2.5 エ:2.8
平均ビット数は、各文字を表すビット数とその出現確率をかけたものを足し合わせて平均ビット数を求めることができます。
平均ビット数の計算
①. 各文字を表すビット数とその出現確率をかける
- A:1ビット × 0.5 = 0.5ビット
- B:2ビット × 0.3 = 0.6ビット
- C:3ビット × 0.1 = 0.3ビット
- D:4ビット × 0.05 = 0.2ビット
- E:4ビット × 0.05 = 0.2ビット
②. ①を合算する
0.5 + 0.6 + 0.3 + 0.2 + 0.2 = 1.8

基本情報技術者試験おすすめの参考書・問題集
| いちばんやさしい 基本情報技術者 | 『基本情報技術者試験』試験に、短期間で一発合格するための試験対策本。ITの知識がまったくない、未経験者やでもスラスラと学習を進められるよう、丁寧に解説。 |
| かやのき先生の基本情報技術者教室 | 基本情報技術者をめざす方のためのやさしいオールインワンタイプの参考書&問題集。イラストや豊富な図解・例え話を駆使して理解しやすく・記憶に残りやすいように説明。 |
| 基本情報技術者 パーフェクトラーニング過去問題集 | 科目A・Bともに万全の対策ができる、定番の過去問題集!科目A・科目Bの両方について万全の対策ができる。 |
| キタミ式イラストIT塾 基本情報技術者 | すべての解説をイラストベースで行っているため,とてもわかりやすい解説本。いちばん最初に読む基本情報技術者試験関連の書籍を探している人におすすめ! |
| 出るとこだけ!基本情報技術者[科目B] | 基本情報技術者【科目B】対策の定番書!前提知識+解き方+試験問題を掲載。効率よく学習できる。 |
| 基本情報技術者 合格教本 | 出題範囲を体系的にきちんと理解しながら学習したい人におすすめ!基本情報技術者試験の定番テキストの改訂版。 |
| 基本情報技術者 超効率の教科書+よく出る問題集 | 動画でスムーズに学習スタート、テキストでしっかり理解度を深める!よく出る問題を反復学習することで、合格に直結するチカラが身に付く! |

