


問題
桁落ちの説明として,適切なものはどれか。
- ア:値がほぼ等しい浮動小数点数同士の減算において,有効桁数が大幅に減ってしまうことである。
- イ:演算結果が,扱える数値の最大値を超えることによって生じる誤差のことである。
- ウ:浮動小数点数の演算結果について,最小の桁より小さい部分の四捨五入,切上げ又は切捨てを行うことによって生じる誤差のことである。
- エ:浮動小数点の加算において,一方の数値の下位の桁が結果に反映されないことである。
基本情報技術者平成27年春期 午前問2
コンピュータで発生する誤差には「丸め誤差」「打切り誤差」「桁落ち」「情報落ち」などがあります。
本記事では「丸め誤差」「打切り誤差」「桁落ち」「情報落ち」について図解で分かりやすく解説していきます。
本記事で学べること
- コンピュータで発生する誤差を理解
- 丸め誤差、打切り誤差、桁落ち、情報落ちの違いを理解
- 基本情報技術者試験の過去問の解き方を学ぶ
目次
コンピュータの誤差
コンピュータで小数を扱う方法の1つに「浮動小数点数」があります。浮動小数点数では、小数で表現できる数の範囲が決まっています。
例えば、32ビット形式の浮動小数点数では、仮数部は24ビットです。

このように、浮動小数点数で小数を表現する場合、表現できる数の範囲が決まっており、限られたビット数で数をあらわします。
スポンサーリンク
そのため、表現できる数の範囲を超えてしまうことがあり(表現できる数の最小値を超えることを"アンダーフロー"、最大値を超えることを"オーバーフロー"という)、表現できる数の範囲を超えてしまった場合、コンピュータはなるべく近い値を使います。その結果、実際の値と誤差が生じてしまいます。
これがコンピュータで発生する誤差です。
コンピュータで発生する誤差には「丸め誤差」「打切り誤差」「桁落ち」「情報落ち」などがあります。
コンピュータで発生する誤差の種類
丸め誤差
丸め誤差とは、コンピュータが「表現できる数の範囲」(有効桁)を超えてしまった際に、「四捨五入」や「切り上げ」「切り捨て」などを行い有効桁以降の値を捨てることにより生じる誤差のことです。
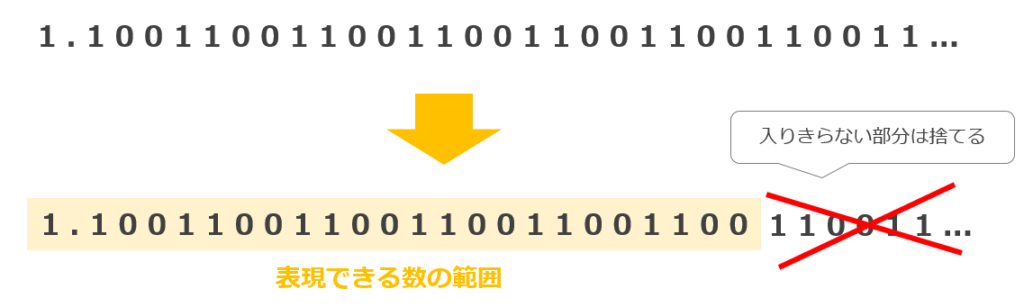
打切り誤差
打切り誤差とは、計算処理を途中で打ち切ることにより発生する誤差のことです。
例えば次のような計算があるとします。※説明のため10進数を例にしています。
1 ÷ 3 = 0.3333333333333...
上記のように無限に続く計算を無限回おこなうわけにはいかないため、途中で計算を打ち切ります。その結果、正しい値との間に誤差が発生します。この時に発生する誤差が「打切り誤差」です。

桁落ち
桁落ちとは、値がほぼ等しい数値の差を求めた時に有効数字が大きく減ることによって生じる誤差のことです。※有効数字:位取りを示すだけのゼロを除いた意味のある数字

例題
値がほぼ等しい31.60696125と31.57530680の差を求めよ。
※有効桁数(表現できる数の範囲)は7桁とする。
(1) 値がほぼ等しい2つの数値の差を求める
まず小数の計算をするため浮動小数点数にします。今回の例では、有効数字は7桁なので7桁に収まらない値は「丸め誤差」により切り捨てます。
浮動小数点数の形式にする
31.60696125 ≒ 0.3160696 × 102
31.57530680 ≒ 0.3157531 × 102
※7桁に収まらない値は四捨五入
浮動小数点数の求め方はこちら
2つの数値の差を求める
差を求める
(0.3160696 × 102) - (0.3157531 × 102) = 0.0003165 × 102
(2) 正規化する
最後に正規化します。正規化とは小数点の位置を調整し最上位桁を0以外の値にする作業のことです。

以下は正規化のイメージ例です。※10進数の例
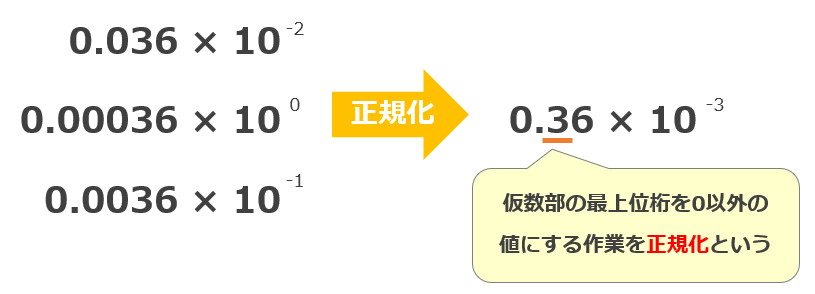
正規化
0.0003165 × 102
↓ 正規化
0.3165000 × 10-1

値がほぼ等しい値の差を求めた結果、有効数字が4桁に減っています。
そして 正規化した結果、仮数部が7桁になるように不足している部分を0で埋めます。このとき付与された「0」は正しい値であるかの保証がないのです。
これが「桁落ち」による誤差です。
スポンサーリンク
ためしに丸め誤差や正規化を考えずに、元データの差を計算してみます。
差を求める
31.60696125 - 31.57530680 = 0.03165445
答えは「0.03165445」です。やはり「0」は正しい値ではありませんでした。
桁落ちによって「0.3165000 × 10-1」となりましたが、本来であれば「0.3165445 × 10-1」が正しい値です。※赤字の個所が桁落ちにより発生した誤差
情報落ち
情報落ちとは、コンピュータで絶対値の大きな値と小さい値の加減算を行った際に、小さい値の情報が無視されてしまうことによって生じる誤差のことです。
例えば、次のような値の和を求めてみます。※有効桁数は4桁で説明のため10進数を例にしています。
大きな値:0.1234 × 102
小さな値:0.1234 × 10-2 = 0.00001234 × 102
手順1 和を求める
0.1234 × 102 + 0.00001234 × 102 = 0.12341234 × 102
手順2 正規化
0.12341234 × 102
↓ 正規化 ※有効桁数は4桁
0.1234 × 102

正規化した結果「0.1234 × 102」となり、小さい数である「0.00001234」はなかったことになっています。これが「情報落ち」です。
基本情報技術者試験 過去問の解説
問題
桁落ちの説明として,適切なものはどれか。
- ア:値がほぼ等しい浮動小数点数同士の減算において,有効桁数が大幅に減ってしまうことである。
- イ:演算結果が,扱える数値の最大値を超えることによって生じる誤差のことである。
- ウ:浮動小数点数の演算結果について,最小の桁より小さい部分の四捨五入,切上げ又は切捨てを行うことによって生じる誤差のことである。
- エ:浮動小数点の加算において,一方の数値の下位の桁が結果に反映されないことである。
基本情報技術者平成27年春期 午前問2
桁落ちとは、値がほぼ等しい数値の差を求めた時に有効数字が大きく減ることによって生じる誤差のことです。
それでは、解答のア~エについてみていきます。
ア:値がほぼ等しい浮動小数点数同士の減算において,有効桁数が大幅に減ってしまうことである。
→ 桁落ちの説明。正解
イ:演算結果が,扱える数値の最大値を超えることによって生じる誤差のことである。
→ オーバーフロー(桁あふれ誤差)の説明。不正解
※例えば「99 + 1 = 100」だが扱える数値の最大値が99の場合、答えが0になってしまう現象。
ウ:浮動小数点数の演算結果について,最小の桁より小さい部分の四捨五入,切上げ又は切捨てを行うことによって生じる誤差のことである。
→ 丸め誤差の説明。不正解
エ:浮動小数点の加算において,一方の数値の下位の桁が結果に反映されないことである。
→ 情報落ちの説明。不正解
基本情報技術者試験おすすめの参考書・問題集
| いちばんやさしい 基本情報技術者 | 『基本情報技術者試験』試験に、短期間で一発合格するための試験対策本。ITの知識がまったくない、未経験者やでもスラスラと学習を進められるよう、丁寧に解説。 |
| かやのき先生の基本情報技術者教室 | 基本情報技術者をめざす方のためのやさしいオールインワンタイプの参考書&問題集。イラストや豊富な図解・例え話を駆使して理解しやすく・記憶に残りやすいように説明。 |
| 基本情報技術者 パーフェクトラーニング過去問題集 | 科目A・Bともに万全の対策ができる、定番の過去問題集!科目A・科目Bの両方について万全の対策ができる。 |
| キタミ式イラストIT塾 基本情報技術者 | すべての解説をイラストベースで行っているため,とてもわかりやすい解説本。いちばん最初に読む基本情報技術者試験関連の書籍を探している人におすすめ! |
| 出るとこだけ!基本情報技術者[科目B] | 基本情報技術者【科目B】対策の定番書!前提知識+解き方+試験問題を掲載。効率よく学習できる。 |
| 基本情報技術者 合格教本 | 出題範囲を体系的にきちんと理解しながら学習したい人におすすめ!基本情報技術者試験の定番テキストの改訂版。 |
| 基本情報技術者 超効率の教科書+よく出る問題集 | 動画でスムーズに学習スタート、テキストでしっかり理解度を深める!よく出る問題を反復学習することで、合格に直結するチカラが身に付く! |

